原子炉物理の基礎（10）原子炉の反応度変化 (03-06-04-10)

＜本文＞
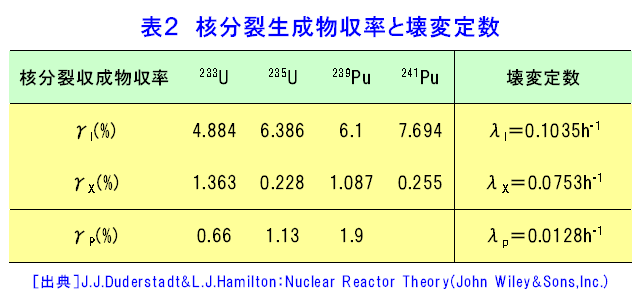
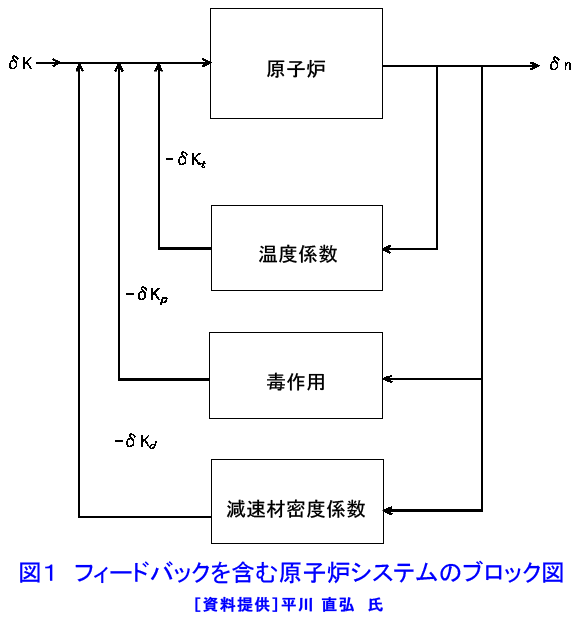
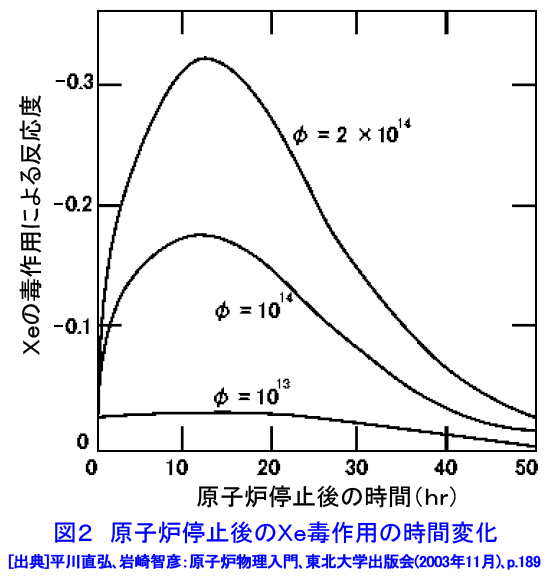
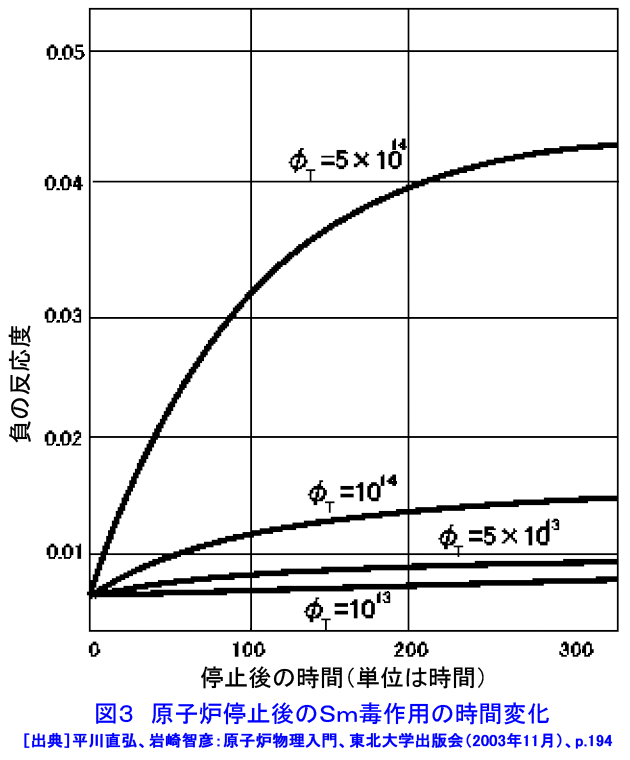
　原子炉には様々な外乱が加えられる。原子炉を運転・操作するための制御棒操作も外乱の一つである。これらの外乱により原子炉の出力が変化し、それは原子炉内の要素の温度変化や圧力変化、核分裂生成物の濃度変化などを引き起こし、それらがさらに反応度変化を引き起こす。図１は水冷却型原子炉について、反応度変化から原子炉出力を変化させるコンポーネント（要素）と、原子炉出力が原子炉の諸状態（この図では温度、冷却材密度、核分裂生成物）の変化により原子炉の反応度が変化する様子を示している。ここでは核分裂生成物の毒作用と反応度温度係数について述べる。（本文中の式の表示については表１参照）

１．核分裂生成物の毒作用
　原子炉運転に伴って核分裂生成物が生成されると、それは４因子公式の中の熱中性子利用率に影響を与える。もともとの原子炉の構成材料のマクロ吸収断面積の和を\(\Sigma_{a}\)、核分裂生成物のマクロ吸収断面積を\(\Sigma_{ap}\)とすると、核分裂生成物の生成による反応度変化は
\[ \delta\rho=-(\frac{\Sigma_{ap}}{\Sigma_{a}})\tag{1}
\] で与えられる。

a Ａ．¹³⁵Xeの毒作用
　核分裂生成物中特に大きな吸収断面積を持つのは¹³⁵Xeで、その断面積は熱中性子に対し〜3x10⁶バーンであり、²³⁵Ｕの核分裂の場合、核分裂から直接（0.3％）、あるいは¹³⁵Teから下記の連鎖を経て生成される。
　 T_1/2＜ 1min.　T_1/2＝6.7h　T_1/2＝9.2h　T_1/2＝2x10⁶y.
¹³⁵Te　　→ 　¹³⁵Ｉ　　→ 　¹³⁵Xe　　→ 　¹³⁵Cs　　→ 　¹³⁵Ba（安定）
　　　　　β−　　　　　　β−　　　　　　β−　　　　　 β−
表２に²³³Ｕ、²³⁵Ｕ、²³⁹Pu、²⁴¹Puの核分裂生成物収率（\(\gamma_{I}\)、\(\gamma_{X}\)）と壊変定数を示す。なお、¹³⁵Teの半減期は短いので、核分裂から直接¹³⁵Ｉが作られるとして良い。¹³⁵Ｉの原子密度を\(I\)、¹³⁵Xeの原子密度を\(X\)、中性子束を\(\varphi\)とすると、\(I\)、\(X\)に対してそれぞれ次の方程式が立てられる（¹³⁵Ｉのミクロ吸収断面積は小さいので無視する）。また、¹³⁵Xeのミクロ吸収断面積を\(\sigma_{x}\)とする。
\[ (\frac{dI}{dt})＝-\lambda_{I}I(t)+\gamma_{I}\Sigma_{f}\varphi\tag{2}
\] \[ (\frac{dX}{dt})＝-\lambda_{x}X(t)-\sigma_{x}X\varphi(t)+\gamma_{x}\Sigma_{f}\varphi+\lambda_{I}I(t)\tag{3}
\] まず、平衡状態においては\((\frac{dI}{dt})＝0\)、\((\frac{dX}{dt})＝0\)とできるので、これから平衡状態の\(X\)の原子数密度が
\[ X_{0}=[\frac{(\gamma_{I}+\gamma_{x})\Sigma_{f}\varphi}{(\lambda_{x}+\sigma_{x}\varphi)}]\tag{4}
\] そして、\((\frac{dn}{dt})＝[\frac{(\rho_{0}-\beta)}{Λ}]n(t)+(\frac{\beta}{\Lambda})n_{0}\)（原子力百科事典<03-06-04-09>の\((20)\)参照）により、これによる反応度変化（毒作用）が
\[ \Delta\rho=-[\frac{\sigma_{x}(\gamma_{I}+\gamma_{x})\Sigma_{f}\varphi}{(\lambda_{x}+\sigma_{x}\varphi)\Sigma_{a}}]\tag{5}
\] と求められる。臨界にある大型炉（洩れが無視できる）では\(\frac{ν\Sigma_{f}}{\Sigma_{a}〜1}\)とできるので、
\[ \Delta\rho=-[\frac{(\gamma_{I}+\gamma_{x})\varphi}{\nu(\frac{\lambda_{x}}{\sigma_{x}+\varphi})}]\tag{6}
\] となり、中性子束が低いとき、すなわち\(\varphi\ll\frac{\lambda_{x}}{\sigma_{x}}\)のときは\(\Delta\rho\)が中性子束に比例し、
逆に\(\varphi\gg\frac{\lambda_{x}}{\sigma_{x}}\)のときは
\[ \Delta\rho\fallingdotseq-\frac{(\gamma_{I}+\gamma_{x})}{\nu}＝0.026\quad(^{235}Uの場合)\tag{7}
\] となる。
　次に原子炉の停止後を考えると、式\((2)\)、\((4)\)で\(\varphi＝0\)となるから
\[ (\frac{dX}{dt})＝-\lambda_{x}X(t)+\lambda_{II}(t)＝-\lambda_{x}X(t)+\lambda_{I}I_{0}\exp(-\lambda_{I}t)\tag{8}
\] となる。\(I_{0}\)、\(X_{0}\)は平衡状態における\(I\)、\(X\)の原子密度である。この微分方程式を解くと
\[ X(t)＝[\frac{\lambda_{I}}{(\lambda_{x}-\lambda_{I})}]I_{0}[\exp(-\lambda_{I}t)-\exp(-\lambda_{x}t)]+X_{0}\exp(-\lambda_{x}t)\tag{9}
\] となる。また反応度変化は
\[ \Delta\rho=-\frac{\sigma_{x}X(t)}{\Sigma_{a}}\tag{10}
\] で与えられる。このときの\(\Delta\sigma\)を図２に示す。この図から分かるように¹³⁵Xeの密度は原子炉停止後、上昇し、約10時間後にピークに至り、その後数10時間かけてゼロに向かって減少していく。この効果は中性子束の高い場合に大きく、中性子束が2x10¹⁴cm^-2s^-1のときにはピーク時の反応度損失が0.33（33％）にも達する。したがってこの場合原子炉停止後しばらくすると、原子炉を数10時間にわたって再起動できなくなる。

Ｂ．¹⁴⁹Smの毒作用
　¹⁴⁹Smは熱中性子に対して約5.9x10⁴バーンの吸収断面積を持ち、原子炉の運転に少なからぬ影響を与える。以下の連鎖に示すように、¹⁴⁹Smは¹⁴⁹Ndから¹⁴⁹Pmを経て作られ、¹⁴⁹Smは安定である。
　　　　　　T_1/2＝2h　　　　 T_1/2＝54h
　　¹⁴⁹Nd　　　→　　　¹⁴⁹Pm　　　→　　　¹⁴⁹Sm（安定）
¹⁴⁹Ndの半減期は¹⁴⁹Pmの半減期に比べ短いので、核分裂から直接¹⁴⁹Pmができるものとし、¹⁴⁹Pm、¹⁴⁹Smの原子密度を\(P\)、\(S\)　\(\sigma_{s}\)を¹⁴⁹Smのミクロ吸収断面積、\(\gamma^{p}\)を核分裂収率とすると、次の生成、消滅に関する方程式ができる。
\[ (\frac{dP}{dt})＝-\lambda_{p}P(t)+\gamma_{p}\Sigma_{f}\varphi\tag{11}
\] \[ (\frac{dS}{dt})＝-\sigma_{s}S(t)+\lambda_{p}P(t)\tag{12}
\] 　平衡時の¹⁴⁹Smの毒作用は\((\frac{dP}{dt})＝0\)、\((\frac{dS}{dt})＝0\)　として求められ、²³⁵Ｕの場合、
\[ \Delta\rho＝-\frac{S_{0}\sigma_{s}}{\Sigma_{a}}＝(\frac{\gamma_{p}\Sigma_{f}}{\sigma_{s}})(\frac{\sigma_{s}}{\Sigma_{a}})\fallingdotseq-\frac{\gamma_{p}}{\nu}＝000463\tag{13}
\] となる（\(S_{0}\)は平衡時の¹⁴⁹Smの原子密度）。また原子炉停止後の毒作用は\(\varphi＝0\)とした
\[ (\frac{dP}{dt})＝-\lambda_{p}P(t)\tag{14}
\] \[ (\frac{dS}{dt})＝\lambda_{p}P(t)
\] を初期条件\(P(0)＝P_{0}\)、\(S(0)＝S_{0}\)に対して解いて\(S(t)\)を求めることにより、反応度変化が
\[ \Delta\rho=-(\frac{\gamma_{p}}{\nu})[1+(\frac{\sigma_{s}\varphi}{\lambda_{p}})\{1-\exp(-\lambda_{p}t)\}]\tag{15}
\] と与えられる。この場合の反応度変化を図３に示す。中性子束が大きくなると負の反応度が大きくなるが（5x10¹⁴cm⁻²s⁻¹）のとき−0.027)、問題なのは、¹⁴⁹Smが安定なため、時間がたっても減らないので、原子炉の起動のためにはそれだけの余剰反応度が必要なことである。

２．反応度の温度効果
　本節では6因子公式をもとに反応度温度係数（温度変化時の温度変化あたりの反応度変化量\(\frac{\Delta\rho}{\Delta{T}}\)）を議論する。反応度の温度係数は\(S(t)＝\nu\Sigma_{f}vn(t)+\Sigma_{(i)}\lambda_{i}C_{i}\)（原子力百科事典<03-06-04-09>参照）から
\[ \frac{d\rho}{dT}＝-(\frac{1}{k^{2}})(\frac{dk}{dT})\fallingdotseq-(\frac{1}{k})(\frac{dk}{dT})\tag{16}
\] で与えられる。6因子公式において高速中性子の洩れない確率と、熱中性子の洩れない確率をまとめて\(P_{NL}\)と書く。すると6因子公式は
\[ k＝\varepsilon{p}\eta{f}・P_{NL}\tag{17}
\] となるので、この対数をとって微分することにより、
\[ \begin{align} (\frac{1}{k})(\frac{dk}{dT})=&(\frac{1}{\varepsilon})(\frac{d\varepsilon}{dT})+(\frac{1}{\eta})(\frac{d\eta}{dT})+(\frac{1}{p})(\frac{dp}{dT})\\ &+(\frac{1}{f})(\frac{df}{dT})+(\frac{1}{P_{NL}})(\frac{dP_{NL}}{dT})\tag{18}
\end{align} \] となる。すなわち反応度温度係数はそれを構成する各々の温度係数の和となる。以下で各々の温度係数を簡単に議論する。
（1）\(\varepsilon\)：温度による変化は小さく\(\frac{d\varepsilon}{dT}〜0\)である。
（2）\(\eta\)：²³⁵Ｕや²³⁹Pu を燃料とする原子炉では小さく\(\frac{d\eta}{dT}〜0\)と考えてよい。
（3）\(p\)：温度上昇により、共鳴吸収断面積の共鳴幅が拡がり（ドップラー効果）吸収が増加する。また、燃料密度の低い液体減速材の原子炉の場合、\(q(E)＝[\frac{\Sigma_{s}(E_{0})}{\Sigma_{t}(E_{0})}]S\exp[-\int_{E}^{E0}\{\frac{\Sigma_{a}(E')}{\Sigma_{t}(E')}\}(\frac{dE'}{E'})]\)（原子力百科事典<03-06-04-07>の式\((14)\)参照）の分母の\(\Sigma_{t}\)が（密度の減少により\(\Sigma_{s}\)が減るので）減少する。これらにより、\(\frac{dp}{dT}\)はかなり大きな負の値を持つ。
（4）\(f\)：均質炉の場合には燃料、減速材の原子密度の温度変化は同じであり、また、多くの場合、吸収断面積は減速材、燃料ともに\(\frac{1}{v}\)特性を持つので、結果として\(\frac{df}{dT}〜0\)である。非均質炉の場合、減速材の密度の減少により\(f\)が増加する。すなわち傾向として\(\frac{df}{dT}>0\)である。しかし、\(f\)は燃料の吸収断面積が温度変化に伴う熱中性子束スペクトルの変化により大きく変わる場合があり、とくに²³⁹Puを燃料とする原子炉では0.3eVにある共鳴吸収の影響で\(\frac{df}{dT}>0\)が大きくなる可能性がある。
（5）\(P_{NL}\)は温度が上がると減速材（冷却材）の密度が減り、拡散係数が大きくなることから洩れが増す傾向がある。その結果\(\frac{dP_{NL}}{dT}<0\)である（炉自体の寸法が増すことによる正の効果より大きい）。ただし、大型の炉の場合もともと\(P_{NL}\)が小さいので、\(\frac{dP_{NL}}{dT}〜0\)と考えて良い。
　これらが総合されて原子炉の温度係数が決まるが、原子炉の安定的な運転のためには\(\frac{dk}{dT}<0\)となることが必要で、特に温度変化がただちに影響する燃料の温度係数が負であることが必要とされる。
　長期にわたる原子炉の運転のためには、燃料の燃焼による減少、親物質からの新たな核燃料物質の生成を考える燃焼解析が必要である。これには数値計算が必要である。

＜図／表＞

＜参考文献＞
（1）平川直弘、岩崎智彦：原子炉物理入門、東北大学出版会（2003年11月）