原子炉物理の基礎（4）中性子拡散方程式の解法（1） (03-06-04-04)

＜本文＞
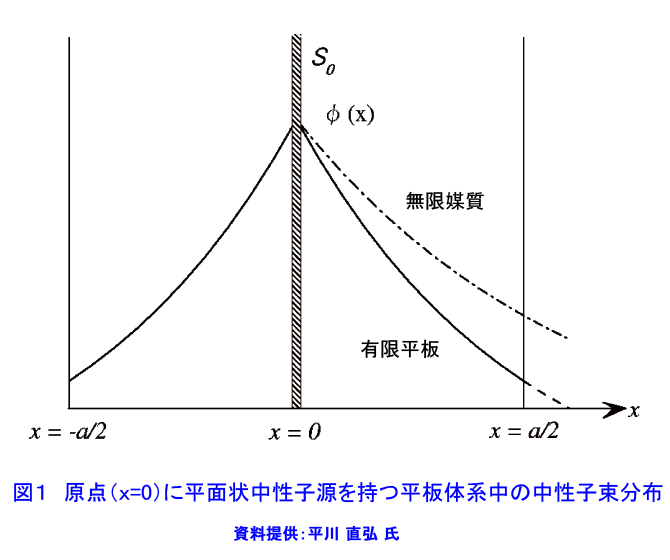
１．非増倍系における中性子拡散方程式の解法
　非増倍系における中性子拡散方程式の解を求める手順は一般的には次の通りである。
（1）中性子源の存在により特異点となる場所以外で成り立つ微分方程式を書く。
（2）一般解を求める。この一般解には2つの任意定数が含まれる。
（3）中性子源の条件を定式化し、これを1つの境界条件とし、これと解の有限性、自由表面での条件等から2つの任意定数を定める。
　以下、無限平板体系、有限平板体系に平面中性子源のある場合と、無限体系中に点状中性子源のある場合について解を求める。（本文中の式の表示については表１-１、表１-２を参照）
　
２．平面状中性子源のある無限体系
　無限に広い体系を考え、その中心に毎秒\(S_{0}\)（個\(/m^{2}\))の割合で中性子を等方的に放出している無限平板状の中性子源があるものとする。この平面源はデイラック（Dirac）の\(\delta\)関数を使って次のように書くことができる。
\[ S(r)＝S_{0}\delta(x) \tag{1}
\] デイラックの\(\delta\)関数は
\[ \delta(x)＝0　x≠0,\quad \int_{-\infty}^\infty\delta(x)dx＝1 \tag{2}
\] となる関数である。
　体系と中性子源が無限に広いことから中性子束は平面源からの距離\(x\)のみの関数であるとすることができる。
　したがって　\(\nabla^2\varphi(r)-(\frac{1}{L^2})\varphi(r)＝−(\frac{1}{D})\varphi(r\))　（ただし、\(L^{2}＝\sqrt{\frac{D}{\Sigma_a}}\)）は、次の形を取る。
\[ \frac{d^2\varphi(x)}{dx^2}−\frac{1}{L^2}＝−\frac{S_{0}}{D}\delta(x) \tag{3-1}
\] 中性子源の存在する\(x＝0\)を除いて、式\((3\)-\(1)\)は
\[ \frac{d^2\varphi(x)}{dx^2}-\frac{1}{L^2}＝0 \tag{3-2}
\] となる。この方程式の一般解は2つの指数関数の和として次のように与えられる。
\[ \varphi(x)＝A\exp(−\frac{x}{L})+C\exp(+\frac{x}{L}) \tag{4}
\] で与えられる。次に任意定数\(A、C\)を定めるため、境界条件を定式化する。
中性子源の幾何学的対称性により、\(x→0\)の時、
\[ \lim_{x \to 0}{J}_{x}^{+}(x)＝−\lim_{x \to 0}{J}_{x}^{−}(x)＝\lim_{x \to 0}{J}_{x}(x)\tag{5}
\] とでき、また\(x＝0\)において中性子源から放出される中性子流は中性子源の強度に等しいから次式となる。
\[ (a)\qquad\lim_{x \to 0}J_{x}(x)＝\frac{S_{0}}{2}\tag{6}
\] 　もう一つの境界条件として体系内で中性子束が有限であることから
\[ (b)\qquad\lim_{x \to \infty}\varphi(x)<\infty\tag{7}
\] 　この2つの境界条件から式\((4)\)の\(A、C\)を決定する。今考えている体系は\(x＝0\)に関して対称であるから\(x>0\)に限って考える。すると境界条件\((b)\)から\(C=0\)
すなわち中性子束は
\[ \varphi(x)＝A\exp(−\frac{x}{L}) \tag{8}
\] となる。境界条件\((a)\)から、\(x→0\)の時
\[ \lim_{x \to 0}{J}_{x}(x)＝\lim_{x \to 0}[-D\frac{d\varphi(x)}{dx}]=\frac{DA}{L}＝\frac{S_{0}}{2}\tag{9}
\] すなわち\(A=\frac{S_{0}L}{2D}\) となる。
したがって求める解は
\[ \varphi(x)=(\frac{S_{0}L}{2D})\exp(-\frac{x}{L})\qquad ( x>0 )\tag{10-1}
\] となる。対称性を考えると
\[ \varphi(x)=(\frac{S_{0}L}{2D})\exp(+\frac{x}{L})\qquad ( x<0 )\tag{10-2}
\] となるから、これらをまとめて無限体系中に平板状中性子源があるときの解は
\[ \varphi(x)=(\frac{S_{0}L}{2D})\exp(-\frac{|x|}{L})\tag{10-3}
\] で与えられる。すなわち、この場合の中性子束は平面源から遠ざかるにつれて体系に固有な拡散距離\(L\)ごとに\(1/e\) になる。また中性子束の大きさは線源の強さ\(S_{0}\)に比例する。これは中性子拡散方程式が線形であることと、重ね合わせの原理により予想される。

３．有限厚さの体系中の中性子束
　次に２．の問題で、\(x\)方向の厚さが有限の場合を考える。体系の厚さを\(a\)とし、その外側は真空であるとする。この場合も拡散方程式は\((3\)-\(1)\)、\((3\)-\(2)\)であり、一般解は\((4)\)である。また境界条件\((a)\)も変わらない。しかし、有限体系ではもう一つの境界条件\((b)\)は「外挿境界において中性子束がゼロ」である。すなわち
\[ (b)\quad \varphi(\pm\frac{a'}{2})＝0 \tag{11}
\] である。ここで\(a’\)は\(\frac{a^{'}}{2}＝\frac{a}{2}\)+\(z0\)で定義される。\(z0\)は外挿距離である。境界条件\((b)\) により\(C\)を消去し、境界条件\((a)\)を用いて\(A\)を定めれば、中性子束は(\(x>0\)の領域において)
\[ \begin{align} \varphi(x)&=\frac{S_{0}L}{2D}\frac{\exp(-\frac{x}{L})-\exp(\frac{(x-a')}{L})}{1+\exp(-\frac{a'}{L})}\\ &=\frac{S_{0}L}{2D}\frac{\sinh\{\frac{(a'-2x)}{2L}\}}{\cosh(\frac{a'}{2L})}\tag{12-1}
\end{align} \] \(x＝0\)における対称性を考慮すると解は最終的に次の形となる。
\[ \varphi(x)=\frac{S_{0}L \sinh \{\frac{(a'-2|x|)}{2L}\}}{2D \cosh(\frac{a'}{2L})} \tag{12-2}
\] 　図１に無限体系および有限体系における中性子束分布の概形を示す。なお、有限な体系ではあらかじめ中性子束の一般解を \[ \varphi(x)=A\cosh(\frac{x}{L})+C\sinh(\frac{x}{L})\tag{13}
\] の形に書いておくと計算が容易となることが多い。

４．無限体系中の点状中性子源
　次に無限体系の中心\((r＝0)\)に毎秒\(S_{0}\)(個\(\cdot s^{−1})\)の割合で中性子を等方的に放出している点状の中性子源がある場合を考える。中性子源が等方的なので中性子束に角度依存性はなく、極座標系を用いると、中性子源を除く領域、すなわち、\(r≠0\)における拡散方程式は
\[ \frac{1}{r^{2}}\frac{d}{dr}r^{2}\frac{d\varphi(r)}{dr}-\frac{1}{L^{2}}\varphi(r)=0\qquad(r>0)\tag{14}
\]
である。極座標系における拡散方程式に対しては、\(\varphi(r)=\frac{u(r)}{r}\)として\((14)\)に代入すると、\(u(r)\)に対する方程式が\((3\)-\(2)\)と同じ形となり、一般解は
\[ \varphi(r) = (\frac{1}{r})[A\exp(-\frac{r}{L})+C\exp(+\frac{r}{L})] \tag{15} \] 　境界条件の一つは中性子源から流れ出る中性子流が中性子源の強さに等しいことである。
\[ (a)\qquad\lim_{r \to 0}4\pi{r}^{2}J(r)=S_{0}\tag{16} \] もう一つの境界条件は中性子束が有限であることである。すなわち
\[ (b)\qquad\varphi(r)<\infty\qquad(r \to \inftyに対して)\tag{17} \] 　境界条件\((b)\)より\(C＝0\)である。境界条件\((a)\)より\(A=\frac{S_{0}}{4\pi D}\) となり、中性子束は
\[ \varphi (r) =(\frac{S_{0}}{4\pi Dr})\exp(-\frac{r}{L})\tag{18} \] で与えられる。
　この式を利用して中性子が発生した点から吸収される点までの距離の2乗の平均値が計算できる。　すなわち、点状中性子源から\(r\)から\(r\)+\(dr\)の距離にある球殻を考えると、この体積は\(4\pi r^{2}dr\)であり、中性子束が\(\varphi (r)\)であるからこの球殻での吸収率は\(4\pi r^{2}\sum_{a} \varphi (r)dr\)となるので、式\((18\))を代入すると \((\frac{S_{0}}{L^{2}})r\exp(-\frac{r}{L})dr\)
　これを\(S_{0}\)で割れば、中性子がこの球殻内で吸収される確率\(p(r)\)が得られ、
\[ p(r)dr = (\frac{1}{L^{2}})r\exp(-\frac{r}{L})dr \tag{19} \] となる。よって中性子が発生した点から吸収される点までの距離の2乗の平均値は
\[ r^{2}=\frac{\int_{0}^{\infty}r^{2}p(r)dr}{\int_{0}^{\infty}p(r)dr}=6L^{2}\tag{20} \] となる。つまり拡散距離\(\ L\ \)は中性子が中性子源から吸収される点までに飛行する直線距離の2乗の平均値の平方根の\(\frac{1}{\sqrt 6}\)　と考えることができる。

＜図／表＞

＜参考文献＞
（1）平川直弘、岩崎智彦：原子炉物理入門、東北大学出版会（2003年11月）