原子炉物理の基礎（9）中性子束の時間的変化 (03-06-04-09)

＜概要＞
　中性子束の時間的変化に関連する問題を述べる。まず、原子炉運転において遅発中性子を考慮する必要性を示す。次に原子炉の制御において中心的役割を占める原子炉動特性方程式を導出し、その応用例を示す。さらに、原子炉制御で考慮する必要のある、反応度に対するXe等の核分裂生成物の影響と反応度温度係数について簡単に述べる。

＜更新年月＞
2006年06月　　　（本データは原則として更新対象外とします。）

＜本文＞
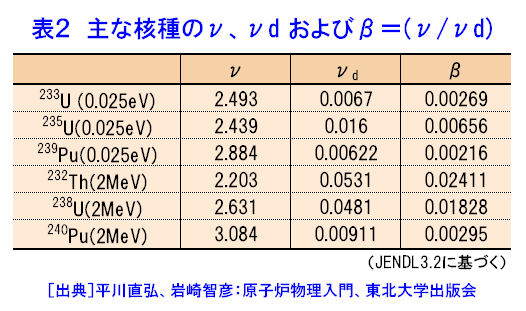
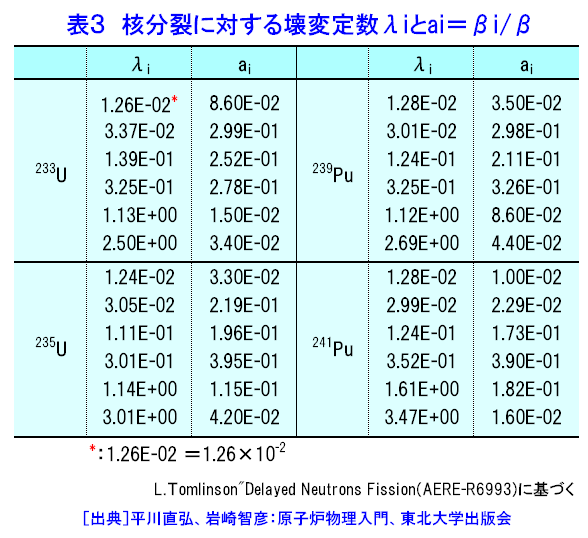
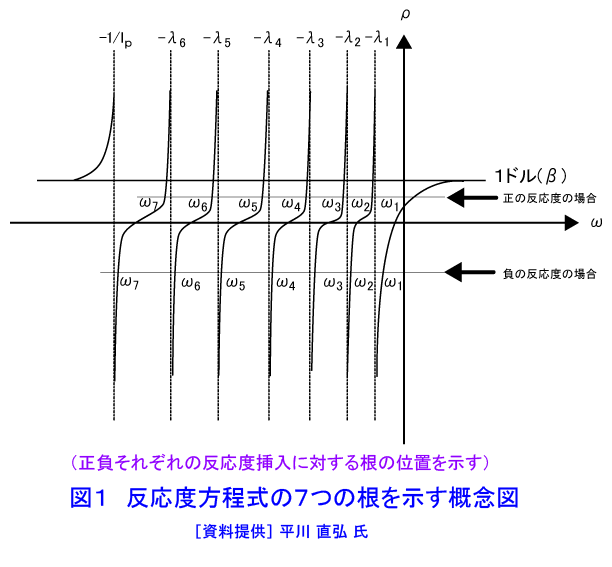
１．遅発中性子の生成機構
　核分裂に伴って2〜3個（²³⁵Ｕの場合は2.42個）の中性子が核分裂直後（10−14秒以内）に放出される。しかし、ごく僅か（1％以内）の中性子がかなりの時間たってから放出される。まず、遅発中性子の生成機構について例をとって説明する。（本文中の式の表示については表１参照）
　多くの核分裂生成物のなかに⁸⁷Brがある。この核は約55秒の半減期でβ−壊変して⁸⁷Ｋの励起状態Kr*になる。壊変で作られた核は、普通γ線を出して基底状態に落ちるが、⁸⁷Kr*の場合、（1）⁸⁷Ｋは中性子数が魔法の数50より1個多い51個で、この51番目の中性子の結合エネルギーが非常に小さい。（2）⁸⁷Kr*は⁸⁷Brの壊変に際して、かなりの割合でこの結合エネルギーより高い励起状態に作られる。
　このため、高い励起状態に生じた⁸⁷Kr* からは中性子が放出され、核は⁸⁶Krとなる。このとき、中性子は⁸⁷Kr* に崩壊した後直ちに発生するが、実際にはあたかも中性子が⁸⁷Br の半減期である55秒の時間遅れを持って生じたように見える。このように核分裂後、時間遅れを持って生ずる中性子を遅発中性子といい、⁸⁷Br のように、遅発中性子を出す核分裂生成物を遅発中性子先行核という。今日約45種類の遅発中性子先行核が知られているが、原子炉物理では通常これを６つのグループに分けている。最も半減期の長い⁸⁷Br が先行核である以外のグループは複数個の先行核をまとめて１グループとしている。表２に熱中性子核分裂に対する²³³Ｕ、²³⁵Ｕ、²³⁹Puの、また高速中性子核分裂に対する²³³Th、²³⁸Ｕ、²⁴⁰Puの発生中性子数（ν）、遅発中性子発生数（ν_d）およびその比で与えられるβを示す。βの違いは主に核分裂生成物の収率曲線の違いによる。表３には²³³Ｕ、²³⁵Ｕ、²³⁹Pu、²⁴¹Puの熱中性子核分裂に対する壊変定数（λ_i:λ_i＝0.693 /T_i）と、a_i＝β_i/βを示す（なお、β＝Σ_（i）β_i　である。以下、Σ_（i）によりiについての和を取ることを示す）。遅発中性子のエネルギーは即発中性子に比べかなり低い。
２．遅発中性子の重要性
　原子炉において中性子の世代時間（核分裂から次の核分裂までの平均時間）をl、中性子増倍率をkとし、中性子数の時間変化を考える。今、t＝0における中性子数をN（0）、t＝tにおける中性子数をN（t）とする。増倍率の定義からN（t＋l）＝kN（t）である。左辺のN（t＋l）をテーラー展開すれば、
　　N（t＋l）≒N（t）＋l（dN/dt）＝kN（t）　・・・（1）
であるから
　　dN/dt＝［（k−1）/l］N（t）　・・・（2）
したがって
　　N（t）＝N（0）exp［−（k−1）/l］　・・・（3-1）
で与えられる。これをしばしば
　　N（t）＝N（0）exp（t/T）　T＝l/（k−1）　・・・（3-2）
と書き、Tをペリオド（原子炉時定数）という。このTは原子炉出力がe倍となる時間である。
　式（3-2）によって原子炉動特性についての簡単な検討を行う。原子炉が臨界にあればk＝1でTは∞であり、N（t）＝N（0）で一定である。この原子炉の増倍率がt＝0で0.1％（1.000から1.001に）変化したとする。lとして熱中性子炉の代表的な値である　＝10^-4秒を取ると、
　T＝10^-4/（1.001−1.000）＝10^-1となり、１秒後の原子炉出力が
　　N（1秒）＝N（0）exp（10t）＝22024N（0）　・・・（4）
となる。すなわち、原子炉出力は１秒後に2万倍以上となり、これを通常考えられる機械装置で制御することはできない。しかし、遅発中性子を考えるとこの事情は一変する。遅発中性子の各組の平均寿命をτ_i（＝1/λ_i）とし、これまでのlを改めてl_pと書くと
　l＝l_p（1−β）＋Σ_（i）β_i（τ_i＋l_p）
　　　≒l_p＋Σ_（i）（β_i/λ_i）≒Σ_（i）（β_i/λ_i）　・・・（5）
とできるので、β_i、λ_i として表２と表３から与えられる値を代入するとΣ（β_i/λ_i）＝0.085 となり、前と同じくk＝1.000からk＝1.001に変化したとすると、T＝0.085/0.001＝85秒となり、この場合、1秒後の出力は
　　N（1秒）＝N（0）exp（1/85）＝1.012N（0）　・・・（6）
すなわち１秒後の出力は1.2％増加するに過ぎず、機械的装置で容易に制御できる。
３．１点炉原子炉動特性方程式の導出
　時間依存拡散方程式（原子力百科事典<03-06-04-03>の式（18）参照）
　（1/v）（∂φ/∂t）＝S（r，t）−Σ_a（r，t）φ（r，t）−∇Ｄ∇φ（ｒ，t）　において　S（r，t）＝S（t）ψ（r）、φ（r，t）＝n（t）ψ（r）とし、また中性子源項を即発中性子項と遅発中性子項に分けて
　　S（t）＝νΣfvn （t）＋Σ_（i）λ_iC_i　・・・（7）
ただしC_i（t）は、
　（dC_i/dt）＝β_iΣ_fvn（t）−λ_iC_i（i＝1，…，6）　・・・（8）
という先行核濃度に関する微分方程式の解とする。
　　　∇²ψ（r）＋B²ψ（r）＝0　・・・（9）
と仮定し、k_∞＝νΣ_f/Σ_a、L²＝D/Σ_a、k＝k_∞/（1＋L²B²）という関係を用い、また即発中性子寿命（prompt neutron lifetime）を次のように定義すると、
　　l＝1/［vΣ_a（1＋L²B²）］　・・・（10）
　（dn/dt）＝｛｛k（1−β）−1｝/l］n（t）＋Σ_（i）λ_iC_i　・・・（11-1）
　（dC_i/dt）＝（k/l）β_in（t）−λ_iC_i （i＝1，…，6）　・・・（11-2）
という連立微分方程式が得られる。これを１点炉動特性方程式という。
　この式は、実効増倍率が１からずれている割合を示す、反応度
　　　ρ＝（k−1）/k　・・・（12）
を用いて書き直すと
　（dn/dt）＝（ρ−β）/Λ＋Σ_（i）λ_iC_i　・・・（13-1）
　（dC_i/dt）＝（β_i/Λ）n（t）−λ_iC_i（i＝1，…，6）　・・・（13-2）
となる。即発中性子寿命lを実効増倍率kで割ったΛは中性子世代時間（neutron generation time）といわれ、２節の始めにlとして定義した量である。
４．１点炉動特性方程式の解
　最も基本的な場合として、t＝0まで臨界状態にあり、一定出力で運転していた原子炉にρ₀というステップ状の反応度が加えられた場合を考える。n（t）＝Aexp（ωt）、C_i（t）＝C_iexp（ωt）としてこれらを式（13-1）と（13-2）に代入すると、反応度方程式
　　ρ₀＝ωΛ＋Σ_（i）［ωβ_i/（ω＋λ_i）］　・・・（14）
が得られる。この方程式の７つの根、ω_j（j＝1，…，7）を用いて中性子密度の時間変化n（t）が
　　n（t）＝Σ_（j）A_jexp（ω_jt）　・・・（15）
で与えられる。ここでωを１/Tに置き換えた式を逆時間方程式（inhour equation）という。
　以下でこの式の応用を考える。
Ａ．正の反応度
　反応度ρ₀を与えたときの、ρ₀と根ω_jとの関係を図１に示す。正のρ₀に対し、一つのみが正で他の根は負であるから、反応度投入後、十分な時間がたった後には、６つの負の指数関数の項は消えて原子炉出力はω₁の項に支配されることが分かる。
すなわち、
　　n（t）→A₁exp（ω₁t）＝A₁exp（t/T）　・・・（16）
これは漸近ペリオドと呼ばれる。
Ｂ．負の反応度
　ρ₀が負の場合、７つのω_jはみな負である。しかしω₁ω₂＞…＞ω₇のため、十分時間が経った時には、中性子束はやはりexp（ω₁t）の形で変化する。しかし負の反応度に対しては、負の反応度の絶対値｜ρ₀｜をいくら大きくしてもω₁が−λ₁より小さくなることはない。すなわちω₁→−λ₁である。このλ₁は表３の第１組の壊変定数であり、おおよそ0.0125s^-1である。したがって大きな負の反応度を挿入した時の原子炉出力の時間変化はexp（−0.0125t）＝exp（−t/80）の形となる。つまり、どんなに大きな負の反応度を与えたとしても原子炉出力を80秒より速いペリオドで低下させることはできない。
Ｃ．大きな正の反応度の添加
　このとき、ω₁≫βであり、反応度方程式（14）においてωに対してλ_iを無視することができる。そこで
　　ρ₀＝ωΛ＋Σ_（i）β_i/（ω＋λ_i）→
　　　　　　ω₁Λ＋ω₁Σ_（i）（β_i/ω₁）＝ωΛ＋β　・・・（17）
ただしΣ_（i）β_i＝β）となり、原子炉ペリオドが
　　T＝1/ω₁＝Λ/（ρ₀−β）＝l/［k（1−β）−1］　・・・（18）
となる。すなわち、ρ₀がβを超えると原子炉の振舞いは即発中性子寿命lで支配される。したがって、原子炉はρ₀＞βの状態とならないようにしなくてはならない。ρ₀＝βの状態を即発臨界という。
Ｄ．即発跳躍近似（prompt jump）
　ステップ状の反応度が投入された直後に限ると、遅発中性子先行核濃度は一定で反応度投入前の値を取るという近似が成り立つ。その先行核濃度をC_i0とすると、式（13-2）で
dCi/dt ＝ 0と置いて、
　　C_i0＝（β_i/λ_iΛ）n₀　（i＝1，…，6）　・・・（19）
である。n₀は反応度投入前（t＜0）での中性子密度である。これを式（13-1）に代入すると
　　（dn/dt）＝［（ρ₀−β）/Λ］n（t）＋（β/Λ）n₀　・・・（20）
となる。これを解くと
　　n（t）＝n₀［｛β/（β−ρ₀）｝−｛ρ₀/（β−ρ₀）｝
　　　　　　　　　　　　　　　　　　　exp｛（ρ₀−β）t/Λ｝］　・・・（21）
となる。即発臨界とならない条件、すなわちρ₀＜βのとき、上の第２項の指数関数内の係数（ρ₀−β）/Λは負で、Λが小さいため大きな絶対値を取る。したがってこの項は急速にゼロに近付き、その結果反応度を加えた直後に原子炉出力は急速に
　　n（t）≒［β/（β−ρ₀）］n₀　　（22）
となる。すなわち、反応度投入直後原子炉出力に急激な変化が起こる。これを即発跳躍という。かりにρ₀が0.001であったとすると、ウラン燃料の熱中性子炉のβは0.0065であるから中性子密度すなわち原子炉出力が0.0065/0.0055＝1.182倍に上昇する。これは原子炉にとって大きな出力上昇である。なお、この近似は負の反応度を投入して制御棒の反応度を測定するのに応用される。
Ｅ．外部中性子源を持つ臨界未満炉
　最後に原子炉が臨界未満の状態にあって外部中性子源Sによって定常状態にあるときを考える。このとき原子炉動特性方程式は次のようになる。
　（dn/dt）＝［（ρ₀−β）/Λ］n（t）＋Σ_（i）λ_iC_i＋S＝0　・・・（23-1）
　（dC_i/dt）＝（β_i/Λ）n（t） − λ_iC_i ＝0　（i＝1，…，6）　・・・（23-2）
ここで未臨界度−｜ρ0｜は一定であるとする。
式（23−2）よりΣ_（i）λ_iC_i＝Σ_（i）（β_i/Λ）n（t）＝（β/Λ）n（t）なので、これを（23-1）に代入して
　　n（t）＝n₀＝−Λ（S/ρ₀　・・・（24）
となる。（ρ₀＜0に注意）。未臨界炉の出力は中性子源強度に比例するとともに、未臨界度に逆比例する。この方法も制御棒の更正に用いられる。

＜図／表＞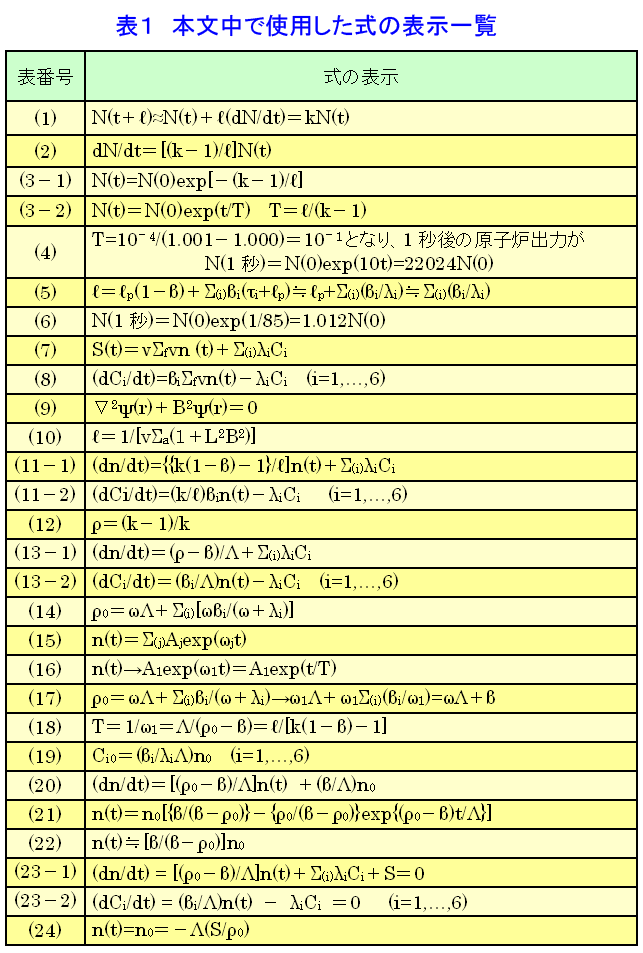
表１本文中で使用した式の表示一覧
表２主な核種のν、νdおよびβ＝（ν/νd）
表３核分裂に対する改変定数λiとai＝βi/β
図１反応度方程式の７つの根を示す概念図

・図表を一括してダウンロードする場合は ここをクリックして下さい。

＜参考文献＞
（1）平川直弘、岩崎智彦：原子炉物理入門、東北大学出版会（2003年11月）