原子炉物理の基礎（7）種々の体系における中性子の減速 (03-06-04-07)

＜本文＞
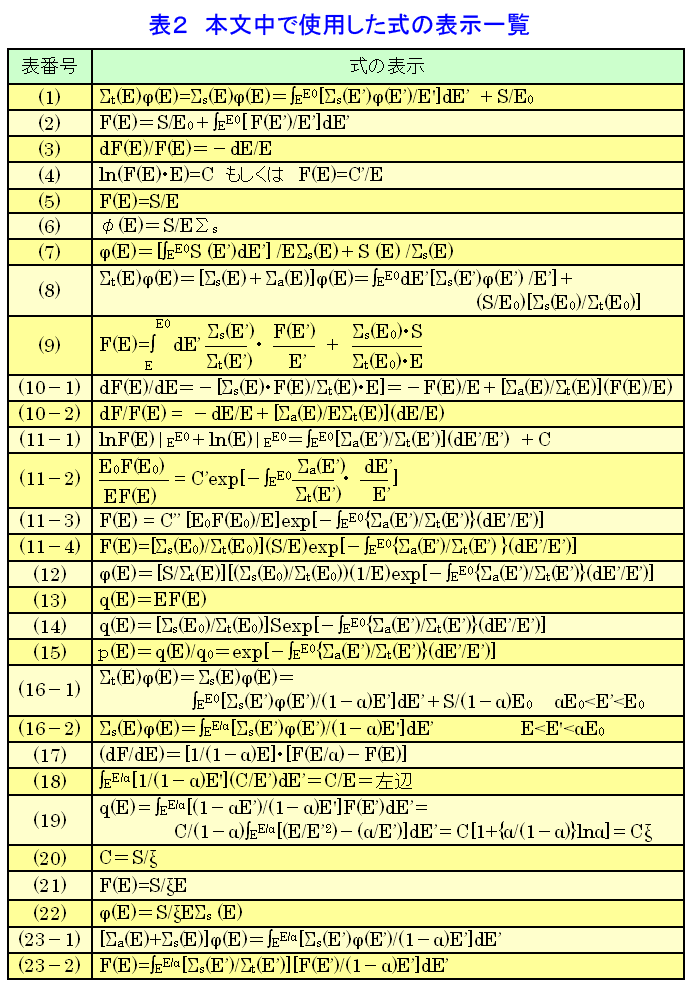
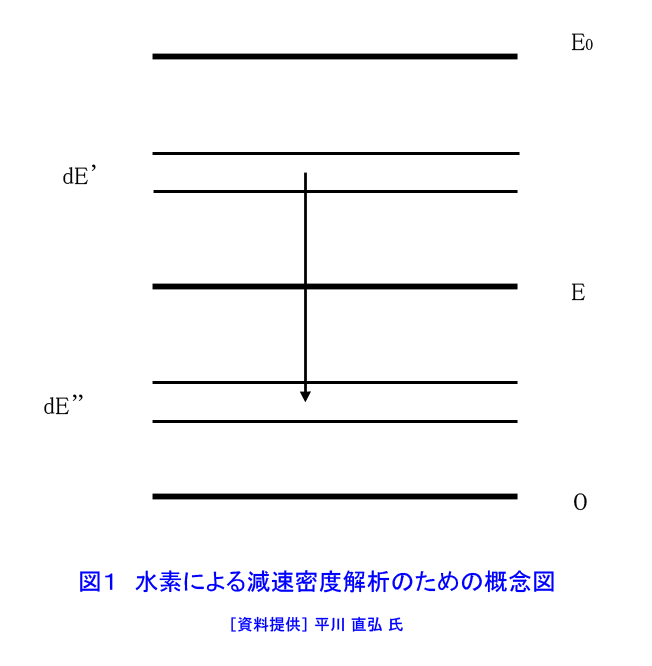
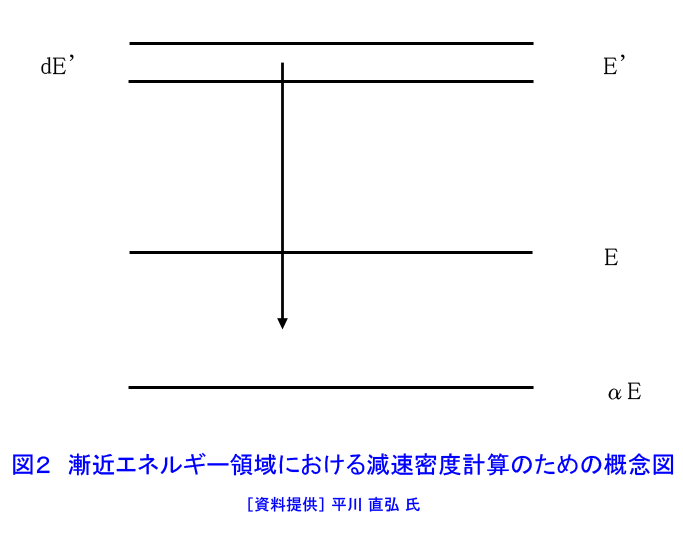
１．無限に広い水素体系中での中性子の減速
　ここでは中性子減速理論（原子力百科事典 03-06-04-06参照）を用いて減速材からなる無限に広い水素体系中での中性子束\(\varphi(E)\)を定めることとする。中性子が原子核との衝突でエネルギーを得ることのない〜1eV以上の領域を対象とする。中性子の減速を検討する際に用いられる用語を表１にまとめた。（本文中の式の表示については表２参照）

1.1　吸収のない場合
　水素の場合、熱エネルギーで\(\frac{\sigma_{a}}{\sigma_{s}}〜0.014\)で、\(\sigma_{a}\)は\(\frac{1}{v}\)に比例するのに対し、\(\sigma_{s}\)はほぼ一定なので、吸収がないという近似は十分妥当である。
　今、エネルギー\(E_{0}\)に単位体積あたり毎秒\(S\)個の割合で中性子を放出する中性子源がある水素体系を考える。すると、エネルギー\(E\)における衝突密度は、それより高いエネルギー\(E'〜E'+dE'\)で衝突（散乱）されて\(E\)にやってくる中性子数に等しいので
\[ \Sigma_{t}(E)\varphi(E)=\Sigma_{s}(E)\varphi(E)=\int_{E}^{E_{0}}[\frac{\Sigma_{s}(E')\varphi(E')}{E'}]dE'+\frac{S}{E}_{0}\tag{1}
\] である。第2項は中性子源での衝突で直接やってくる中性子を示す。この方程式を中性子減速方程式という。衝突密度\(F(E)\)を用いると
\[ F(E)=\frac{S}{E_{0}}+\int_{E}^{E_{0}}[\frac{F(E')}{E'}]dE'\tag{2}
\] となる。この式を微分して書き直すと、 \[ \frac{dF(E)}{F(E)}=-\frac{dE}{E}\tag{3}
\] 　これを積分すれば
\[ ln(F(E)・E)=C\quadもしくは\quad{F}{E}=\frac{C'}{E}\tag{4}
\] が得られる。式\((2)\)で\(E=E_{0}\)とすると\(F(E_{0})=\frac{S}{E_{0}}\)なので定数は\(C'＝S\)と定まる。すなわち、
\[ F(E)＝\frac{S}{E}\tag{5}
\] 　また、中性子束は、次式のようになる。
\[ \varphi(E)=\frac{S}{E\Sigma_{s}}\tag{6}
\] 　もし中性子源が単一のエネルギーでなく、分布\(S(E)\)を持っていたとすると、
\[ \varphi(E)=\frac{[\int_{E}^{E_{0}}S(E')dE']}{E\Sigma_{s}(E)}+\frac{S(E)}{\Sigma_{s}(E)}\tag{7}
\]
1.2　吸収のある場合
　次に水素減速材中に²³⁸Ｕのような吸収性の原子核がある場合を考える。吸収核の散乱断面積はゼロでなく、吸収核による散乱も考えられるが、吸収核の中性子散乱断面積は水素のそれと比べて十分小さくまた原子核を「無限に重い」と近似できるので吸収核による散乱では中性子のエネルギーが変らないとして、吸収核による中性子の散乱を無視する。この場合の減速方程式は
\[ \begin{align} \Sigma_{t}(E)\varphi(E)&=[\Sigma_{s}(E)+\Sigma_{a}(E)]\varphi(E)\\ &=\int_{E}^{E_{0}}dE'[\frac{\Sigma_{s}(E')\varphi(E')}{E'}]+(\frac{S}{E_{0}})[\frac{\Sigma_{s}(E_{0})}{\Sigma_{t}(E_{0})}] \end{align} \tag{8}
\] 積分の部分を\(\Sigma_{s}(E')=\Sigma_{t}(E')-\Sigma_{a}(E')\)を用いて書き直し、
\(F(E)=\Sigma_{t}(E)\varphi(E)\)を用いると
\[ F(E)=\int_{E}^{E_{0}}dE'\frac{\Sigma_{s}(E')}{\Sigma_{t}(E')}・\frac{F(E')}{E'}+\frac{\Sigma_{s}(E_{0})・S}{\Sigma_{t}(E_{0})・E}\tag{9}
\] これを微分して
\[ \frac{dF(E)}{dE}=-[\frac{\Sigma_{s}(E)・F(E)}{\Sigma_{t}(E)・E}]＝-\frac{F(E)}{E}+[\frac{\Sigma_{a}(E)}{\Sigma_{t}(E)}](\frac{F(E)}{E})\tag{10-1}
\] すなわち
\[ \frac{dF}{F(E)}=-\frac{dE}{E}+[\frac{\Sigma_{a}(E)}{E\Sigma_{t}(E)}](\frac{dE}{E})\tag{10-2}
\] これを積分して、
\[ lnF(E)|_{E}^{E_{0}}+ln(E)|_{E}^{E_{0}}=\int_{E}^{E_{0}}[\frac{\Sigma_{a}(E')}{\Sigma_{t}(E')}](\frac{dE'}{E'})+C\tag{11-1}
\] すなわち、
\[ \frac{E_{0}F(E_{0})}{EF(E)}=C'\exp[-\int_{E}^{E_{0}}\frac{\Sigma_{a}(E')}{\Sigma_{t}(E')}・\frac{dE'}{E'}]\tag{11-2}
\] となり、\(F(E)\)は
\[ F(E)＝C''[\frac{E_{0}F(E_{0})}{E}]\exp[-\int_{E}^{E_{0}}{\frac{\Sigma_{a}(E')}{\Sigma_{t}(E')}}(\frac{dE'}{E'})]\tag{11-3}
\] で与えられる。さらに\(E＝E_{0}\)のとき\(F(E_{0})=[\frac{\Sigma_{s}(E_{0})}{\Sigma_{t}(E_{0})}](\frac{S}{E_{0}})\)であるから、これを式\((11\)-\(3)\)と比較することにより\(C''＝S\)となり
\[ F(E)=[\frac{\Sigma_{s}(E_{0})}{\Sigma_{t}(E_{0})}](\frac{S}{E})\exp[-\int_{E}^{E_{0}}\{\frac{\Sigma_{a}(E')}{\Sigma_{t}(E')}\}(\frac{dE'}{E'})]\tag{11-4}
\] となる。この式で\(\Sigma_{a}(E)=0\)とすれば\(F(E)=\frac{S}{E}\)となり、前の結果に一致する。
　また、中性子束は
\[ \varphi(E)=[\frac{S}\Sigma_{t}(E)]・[(\frac{\Sigma_{s}(E_{0})}{\Sigma_{t}(E_{0})})(\frac{1}{E})\exp[-\int_{E}^{E_{0}}\{\frac{\Sigma_{a}(E')}{\Sigma_{t}(E')}\}(\frac{dE'}{E'})]\tag{12}
\] となる。これが吸収体を含む水素減速材中での中性子スペクトルを与える。
　減速材が水素の場合、表１の（ｂ）式で与えられる減速密度（図１参照）は、
\[ q(E)=EF(E)\tag{13}
\] となる。吸収のない場合、式\((5)\)を用いると\(q(E)=S＝q_{0}\)となり、これは中性子源からでた中性子数とあるエネルギーを減速されていく中性子数は等しいので当然である。
　吸収のある場合、式\((13)\)に、式\((11\)-\(4)\)を代入すると、
\[ q(E)=[\frac{\Sigma_{s}(E_{0})}{\Sigma_{t}(E_{0})}]S\exp[-\int_{E}^{E_{0}}\{\frac{\Sigma_{a}(E')}{\Sigma_{t}(E')}\}(\frac{dE'}{E'})]\tag{14}
\] となる。\({q(E)}q_{0}\)という比は源中性子が\(E_{0}\)から\(E\)まで減速される間に吸収されない確率を表わす。吸収が殆ど重い核の共鳴吸収で起こることを考えると、これを「共鳴吸収を逃れる確率\(p(E)\)」と考えることができる。すなわち共鳴吸収を逃れる確率が次式で表される。
\[ p(E)=\frac{q(E)}{q_{0}}=\exp[-\int_{E}^{E_{0}}\{\frac{\Sigma_{a}(E')}{\Sigma_{t}(E')}\}(\frac{dE'}{E'})]\tag{15}
\]

２．\(A>1\)の減速材体系中での中性子の減速
2.1　吸収のない場合
　エネルギー\(E_{0}\)で単位体積、単位時間あたり\(S\)個の中性子が発生しているとすると、この場合の減速方程式は次のようになる。
\[ \begin{align} \Sigma_{t}(E)\varphi(E)=&\Sigma_{s}(E)\varphi(E)=\int_{E}^{E_{0}}[\frac{\Sigma{s}(E')\varphi(E')}{(1-\alpha)E'}]dE'+\frac{S}{(1-\alpha)E_{0}}\\ &\alpha{E}_{0}<{E'}<{E_{0}}\tag{16-1}
\end{align} \] \[ \begin{align} \Sigma_{s}(E)\varphi(E)＝&\int_{E}^{\frac{E}{\alpha}}[\frac{\Sigma_{s}(E')\varphi(E')}{(1-\alpha)E'}]dE'\\ &{E}<{E'}<\alpha{E}_{0}\tag{16-2}
\end{align} \] 　この場合、水素減速材のときと同じように\(F(E)=\Sigma_{s}(E)\varphi(E)\)と置いて微分すると
\[ (\frac{dF}{dE})=[\frac{1}{(1-\alpha)}E]・[F(\frac{E}{\alpha})-F(E)]\tag{17}
\] となり、\(F(\frac{E}{\alpha})\)という項が入る。また\(F(E)\)、またはその微分は中性子が\(n\)回の衝突で減速されるときの最低のエネルギーである\(\alpha^{n}E_{0}\)で不連続となるため、解法は複雑となる。
　そのため、中性子源から遠く離れ、中性子源からの影響が無視できるようになった領域での\((16\)-\(2)\)の解についてのみ考えることとする。この領域を漸近領域という。\((16\)-\(2)\)において(\(F(E)=\Sigma_{s}(E)\varphi(E)\)とした後）\(F(E)＝\frac{C}{E}\)とおいて右辺に代入すると
\[ \int_{E}^{\frac{E}{\alpha}}[\frac{1}{(1-\alpha)}E’](\frac{C}{E'})dE'=\frac{C}{E}=左辺\tag{18}
\] となるので、これが解であることが分かる。定数\(C\)は次のようにして定めることができる。
　図２のように\(E'\)のまわりの\(dE'\)内で散乱された中性子が\(E\)以下のエネルギーに減速される確率は
\(\frac{(E-\alpha{E'})}{(1-\alpha)E'}\)であるから、単位時間、単位体積あたりに\(dE'\)から\(E\)以下のエネルギーに減速される中性子の数、すなわち減速密度は
\[ \begin{align} q(E)&=\int_{E}^{\frac{E}{α}}[\frac{(1-\alpha{E'})}{(1-\alpha)E'}]F(E')dE'\\ &=\frac{C}{(1-\alpha)}\int_{E}^{\frac{E}{α}}[(\frac{E}{E'^{2}})-(\frac{\alpha}{E'})]dE'\\ &=C[1+\{\frac{\alpha}{(1-\alpha)}\}ln{\alpha}]=C\xi\tag{19}
\end{align} \] ここで\(\xi\)についての表１の（ｄ）式を用いた。
　吸収のない無限に広い体系中での減速密度は\(q=S\)であるから、
\[ C=\frac{S}{\xi}\tag{20}
\] となり、衝突密度\(F(E)\)、中性子束\(\varphi(E)\)はそれぞれ次のように与えられる。
\[ F(E)=\frac{S}{\xi{E}}\tag{21}
\] \[ \varphi(E)=\frac{S}{\xi{E}\Sigma{s}(E)}\tag{22}
\]
2.2　吸収のある場合の減速
　式\((16\)-\(2)\)に吸収を導入すると、
\[ [\Sigma_{a}(E)+\Sigma_{s}(E)]\varphi(E)=\int_{E}^{\frac{E}{\alpha}}[\frac{\Sigma_{s}(E')\varphi(E')}{(1-\alpha)E'}]dE'\tag{23-1}
\] または
\[ F(E)=\int_{E}^{\frac{E}{\alpha}}[\frac{\Sigma_{s}(E')}{\Sigma_{t}(E')}][\frac{F(E')}{(1-\alpha)E'}]dE'\tag{23-2}
\] となる。この式は\([\frac{\Sigma_{s}(E)}{\Sigma_{t}(E)}]\)という因子があるため、一般的に解を得ることはできず、数値解法によるか、\(\varphi(E)\)に近似を行うこととなる。

＜図／表＞

＜参考文献＞
（1）平川直弘、岩崎智彦：原子炉物理入門、東北大学出版会（2003年11月）