原子炉物理の基礎（2）中性子増倍率と転換、増殖 (03-06-04-02)

＜本文＞
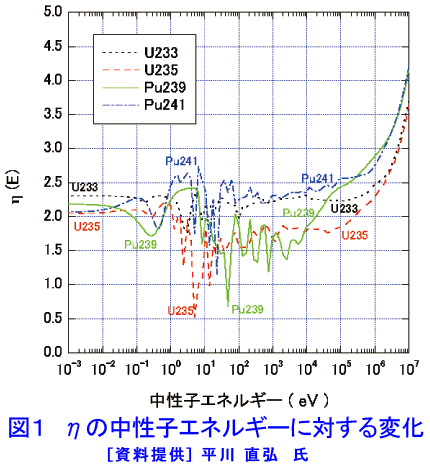
　核分裂によって生まれた中性子が再び核分裂を起こして次の中性子を生み出すまでを、世代という。世代間の中性子の数の比を\(k\)として次のように定義する。
\[ k＝\frac{(ある世代の中性子数)}{(一つ前の世代の中性子数)}\tag{1}
\] \(k\)は増倍率（multiplication factor）と呼ばれる。\(k<1\)の状態を臨界未満（subcritical）、\(k=1\)の状態を臨界（critical）、\(k>1\)の状態を臨界超過（super-critical）という。
　増倍率\(k\)は次式で表される。
\[ k＝\nu{P}_{aF}・P_{f}・P_{NL}\tag{2}
\] ここで、\(\nu\)：核分裂で発生する中性子の数、\(P_{aF}\)：中性子が冷却材や構造材に吸収されずに燃料に吸収される割合、\(P_{f}\)：核燃料物質に吸収された中性子が核分裂を起こす割合、\(P_{NL}\)：中性子が体系外に漏れずに吸収される割合。

１．4因子公式と6因子公式

1.1 無限増倍率
　上述した\(k\)を定量的に表すことを考える。無限に大きい体系とすると、中性子が体系から漏れることはないため、\(P_{NL}=1\)、したがって
\[ k＝\nu・{P_{aF}}・P_{f}\tag{3}
\] この場合の\(k\)を無限増倍率（infinite multiplication factor）といい\(k_{\tiny\infty}\)と書く。この\(k_{\tiny\infty}\)は炉心の大きさ、形状に無関係で、炉心の構成材料の性質と配置のみによる量であり、原子炉の基本的特性を理解する上で特に有用なパラメータである。なお、有限の体系においては\(P_{NL}<1\)であるため、原子炉が臨界となるためには\(k_{\tiny\infty}\)\(>1\)となる必要がある。

1.2 熱中性子利用率
　まず、\(P_{aF}\)について考える。燃料のマクロ吸収断面積を\(\Sigma_{aF}\)、燃料を含む体系の全ての物質のマクロ吸収断面積の和を\(\Sigma_{a}\)と表すと、\(P_{aF}\)は両者の比、すなわち
\[ P_{aF}=\frac{\Sigma_{aF}}{\Sigma_{a}}\tag{4}
\] である。ここで、\(\Sigma_{a}\)のように大文字添字（上の例では\(_{F}\)）がない場合は、その断面積が体系内の全ての物質の和を表す（体系が非均質の場合には、マクロ断面積を適当に空間平均して求めることが必要である）。
　原子炉開発の黎明期には、ほとんどの核分裂は熱中性子によって引き起こされると考えられており、原子炉物理ではこの量を熱中性子利用率（thermal utilization factor）と呼び、\(f\)という記号を用いている。
\[ f=P_{aF}\tag{5}
\] しかし、式\((1)\)の表現は、高速炉のように、核分裂が熱中性子以外で起こる原子炉に対しても成り立つ一般的な表現である。

1.3　\(\eta\)（イータ）
　次に\(P_{f}\)について考える。この量は中性子が核燃料に吸収されたときに核分裂を起こす割合であり
\[ P_{f}＝(\frac{\Sigma_{fF}}{\Sigma_{aF}})=(\frac{\sigma_{fF}}{\sigma_{aF}})\tag{6}
\] と表される。　核分裂に際して平均\(\nu\)個の中性子が放出されるので、核燃料により中性子が再生される割合を記号\(\eta\)を用いて次のように定義する。
\[ \eta=\frac{(\nu\sigma_{fF})}{\sigma_{aF}}＝\nu{P_{f}}\tag{7}
\] \(\eta\)は、再生率（reproduction factor）と呼ばれる場合がある。

1.4 高速中性子核分裂因子\((\varepsilon)\)
　上の議論から無限増倍率は
\[ k_{\tiny\infty}=\eta・f\tag{8}
\] と表すことができる。一方、低濃縮ウランを用いる軽水減速炉や天然ウランを用いる黒鉛減速炉、重水炉などでは、この公式に2つの修正を加えなくてはならない。まず、平均2MeVというエネルギーを持つ高速の核分裂中性子によって、²³⁸Ｕなどの核が核分裂を起こすことを考慮する必要がある。この核分裂は、その世代の中性子数（減速を始める前の中性子の数）を少し増す。この効果を表す量を高速中性子核分裂因子（fast fission factor）と呼び、次のように定義する。
\[ \varepsilon＝\frac{(高速および熱中性子核分裂による全核分裂中性子数)}{(熱中性子核分裂による核分裂中性子数)}\tag{9}
\] この量は1に近く、ほとんどの場合、\(\varepsilon\)＝1.02から1.08の間にある。

1.5 共鳴を逃れる確率
　次に核分裂中性子が生まれたエネルギーから熱中性子エネルギーにまで減速する間に吸収されることを考慮しなくてはならない。この吸収は主に²³⁸Ｕのような重い核種による共鳴吸収によって引き起こされ、共鳴吸収を受けずに熱中性子領域まで減速される割合を共鳴を逃れる確率（resonance escape probability）と呼び、\(p\)で表す。すなわち
\[ p=\frac{(減速を始めた中性子のうち捕獲されずに熱中性子領域まで減速される中性子)}{(減速を始めた中性子数)}\tag{10}
\] と定義される。この量は燃料と減速材の割合に大きく依存するとともに、非均質の熱中性子炉の体系の場合には、その形状、配列に強く依存する。軽水減速炉の場合には、0.6〜0.8の程度である。
　天然ウラン黒鉛炉の場合、もし燃料と減速材が均質に混合されていると\(\eta\)＝1.34、\(\varepsilon\)＝1.02の程度である。また\(p\)と\(f\)の積は最大でも0.63の程度で、\(k_{\tiny\infty}\)は高々0.85の程度にしかならず、原子炉を臨界とすることができない。しかし、天然ウランを塊状にして黒鉛のなかにうまく配置することにより、\(p\)と\(f\)の積を0.79程度にすることができ（\(\varepsilon\)も1.03程度となる）、\(k_{\tiny\infty}\)の最大値を1.09程度にして原子炉を臨界とすることが可能となる。
　上に定義された4つの因子を用いると無限増倍率\(k_{\tiny\infty}\)は
\[ k_{\tiny\infty}=\varepsilon・p・\eta・f\tag{11}
\] と書ける。この無限増倍率を表す式を4因子公式（four-factor formula）と呼ぶ。したがって無限増倍率\(k_{\tiny\infty}\)を求めるためには、それを構成する4つの因子をそれぞれ計算すればよいこととなる。

1.6 6因子公式
　有限体系においては中性子が体系から漏れない確率\(P_{NL}\)を考慮しなくてはならない。この量は原子炉の形状にも依存するが、高速（減速中の）中性子と熱中性子とでは漏れの割合が一般に著しく異なるので、\(P_{NL}\)を高速中性子が漏れない確率\(P_{FNL}\)と、熱中性子が漏れない確率\(P_{TNL}\)の2つに分け、
\[ k＝\varepsilon・p・\eta・f・P_{FNL}・P_{TNL}＝k_{\tiny\infty}・P_{FNL}・P_{TNL}]\tag{12}
\] という6つの因子で表されることとなる。この式を6因子公式（six-factor formula）という。この場合の\(k\)を実効増倍率（effective multiplication factor）という。\(P_{FNL}\)と\(P_{TNL}\)に対する式は、2群拡散理論によると
\[ P_{FNL}＝\frac{1}{(1+{L_{F}}^{2}B^{2})}\tag{13-1}
\] \[ P_{TNL}＝\frac{1}{(1+{L_{T}}^{2}B^{2})}\tag{13-2}
\] で与えられる。ここで\(L_{F}^{2}\)は高速中性子に対する拡散面積、\(L_{T}^{2}\)は熱中性子に対する拡散面積と呼ばれる量である。また、\(B^{2}\)は幾何学的バックリング（geometrical buckling）と呼ばれ、炉心の形状と大きさによって決まる量である。半径\(R\)の球、一辺の長さが\(a\)、\(b\)、\(c\)の直方体、半径が\(R\)で高さが\(H\)の体系に対する幾何学的バックリングを表１に示す。
　もともとこの式は炉心のみからなる、裸の原子炉といわれるものに対する式で、実際の原子炉では炉心の周囲に反射体があるため、この式をそのまま実効増倍率の計算に用いることはできない。ただし、反射体の効果を実効的に炉心が大きくなったと考えて補正を行えば、このように簡単な式でも、電子計算機を用いた、より厳密な計算を行なう前におおよその値を得ることができる。

1.7 臨界量
　式\((12)\)を\((13\)-\(1)\)、\((13\)-\(2)\)を用いて書き直せば、実効増倍率\(k\)は
\[ k＝\frac{k_{\tiny\infty}}{[(1+{L_{F}}^{2}B^{2})(1+{L_{T}}^{2}B^{2})]}\tag{14}
\] となる。原子炉が臨界状態にある場合、\(k＝1\)であるため、
\[ \frac{k_{\tiny\infty}}{\{(1+{L_{F}}^{2}B^{2})(1+{L_{T}}^{2}B^{2})\}}＝1\tag{15}
\] と書くことができる。これを2群理論の臨界方程式という。\(k_{\tiny\infty}\)、\({L_{F}}^{2}\)、\({L_{T}}^{2}\)が与えられれば、この式を解いて\(B^{2}\)を定めることができる。\(B^{2}\)は原子炉の形状に応じて表１で与えられるため、これにより原子炉がちょうど臨界となる寸法を定めることができる。臨界となるときの原子炉の体積を臨界体積、その際、体系中にある燃料の量を臨界量（または臨界質量critical mass）という。式\((15)\)から求められるのは表１に幾何学的バックリングが与えられている場合に対するものであるが、一般に体系の代表的な寸法、たとえば球の半径を\(R\)とすると、中性子の漏れは表面積\(R^{2}\)に比例し、一方、中性子の発生は体積\(R^{3}\)に比例するから、漏れの割合対発生の割合という比は、\(\frac{1}{R}\)に比例すると考えられる。したがって、\(k_{\tiny\infty}>1\)であれば、どんな場合にも\(R\)を増減させることによって、\(k＝1\)という状態を実現する原子炉の寸法を定めることができる。なお、一定の体積に対し、表面積が最小になるのは球の場合であるから、球形の炉心に対する臨界量が最小の臨界量となる。

２．転換と増殖
　天然にある原子核のうち遅い中性子に対し核分裂を起こすのは天然ウランに約0.7％しか含まれていない²³⁵Ｕのみである。しかし、これまで述べてきたように、1個の中性子が燃料に吸収されると\(\eta\)個の中性子を生ずる。臨界状態において、そのうちの1個は次の核分裂を起こすのに必要であるため、残りの\(\eta-1\)個の中性子を²³⁸Ｕや²³²Thのような親物質に吸収させて、熱中性子に対して核分裂を起こす²³⁹Puや²³³Ｕを作れば、利用できる核燃料の量を飛躍的に増大させることができる。これを転換（conversion）という。現実に²³⁸Ｕを含む原子炉では多かれ少なかれこの反応が起こっている。
　さらに、\(\eta-1\)が1より大きい場合、核分裂性核種が1個消費されるのに対し、1個以上の核分裂性核種が作られることになるため、消費した核分裂物質核種以上の核分裂性核種を作ることが可能となる。これを増殖（breeding）といい、これを実現して利用可能な核燃料の量を高めることを目的とする原子炉（増殖炉）の研究が進められている。
　図１に²³³Ｕ、²³⁵Ｕ、²³⁹Pu、²⁴¹Puに対する\(\eta\)のエネルギー変化を示す。この図からわかるように、熱中性子に対する\(\eta\)は²³⁵Ｕや²³⁹Puに対しては2を僅かに超える程度であり、さらにその上のエネルギー領域で\(\eta\)が2を大きく切る領域があるため、中性子の漏れや構造材、冷却材等による吸収を考えると、増殖をさせることは難しい。
　しかし、中性子エネルギーが100keVを超えると、\(\eta\)はエネルギーとともに急激に増加するため、\(\eta>2\)の状態を実現できる可能性がある。特に、²³⁹Puに対しては期待を持つことができる。増殖を実現するためには中性子のエネルギーをできるだけ高く保つことが有効な手段である。この方法により、\(\eta>2\)を実現することを狙った原子炉が、高速増殖炉（fast breeder reactor）である。高速増殖炉では中性子エネルギーを100keV以上に保つために、中性子を減速させる物質を用いることができない。そのため、冷却材として液体金属（ナトリウムが主流）が用いられることとなる。このナトリウムの使用の他、高いエネルギー領域では、核分裂断面積が小さくなること、²³⁸Ｕの非弾性散乱による減速の効果を小さくすることのために、濃縮度の高い燃料を使う必要がある。その結果、経済性の面から、原子炉の単位体積あたりの出力を高くすることが要求されるなど、高速炉の開発には熱中性子炉にはない技術的困難がある。また、原子炉物理の面でも、式\((8)\)のような簡易的な式を直接適用できない。通常、高速炉の解析は数値計算に頼ることとなる。
　なお、²³³Ｕについては熱中性子に対し\(\eta\)＝2.29であり、その上のエネルギー領域でも\(\eta\)が2よりあまり小さくなることがないため、熱中性子炉で増殖を実現させる可能性がある。しかし、そのためには、例えば吸収断面積の大きい核分裂生成物を連続的に炉から取り除く工夫をする必要があること等の技術的困難がある。

＜図／表＞

＜参考文献＞
（1）平川直弘：原子炉物理入門、東北大学出版会（2003年12月）
（2）W.マーシャル（編）、住田健二（監訳）：原子炉技術の発展［上］、（株）筑摩書房（1986年9月30日）
（3）W.マーシャル（編）、住田健二（監訳）：原子炉技術の発展［下］、（株）筑摩書房（1986年10月30日）