原子炉の炉心核設計概論 (03-06-01-04)

＜本文＞
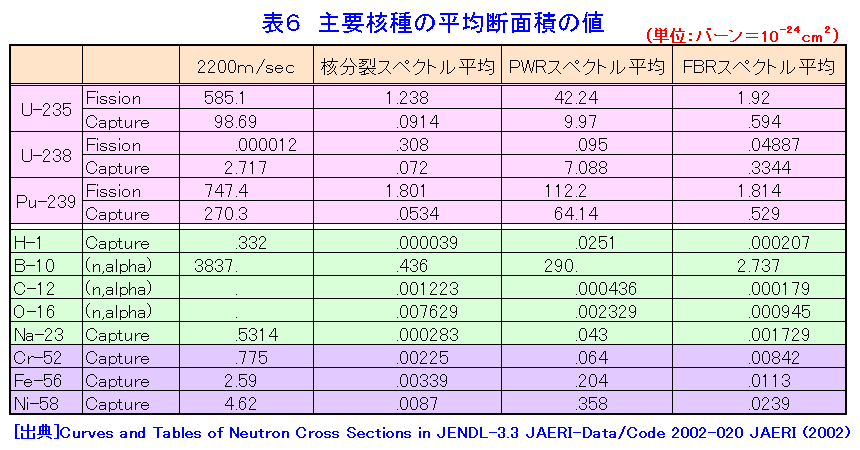
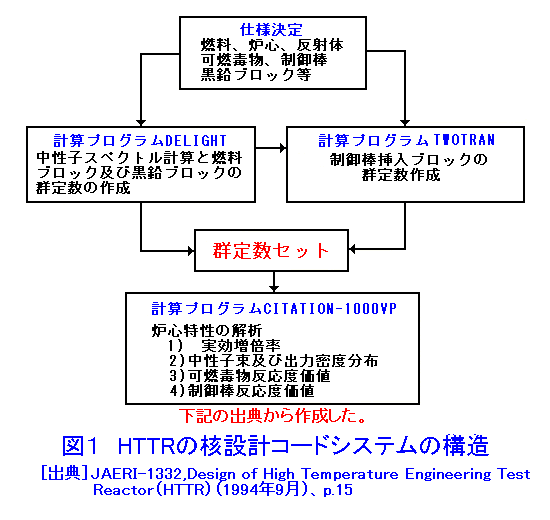
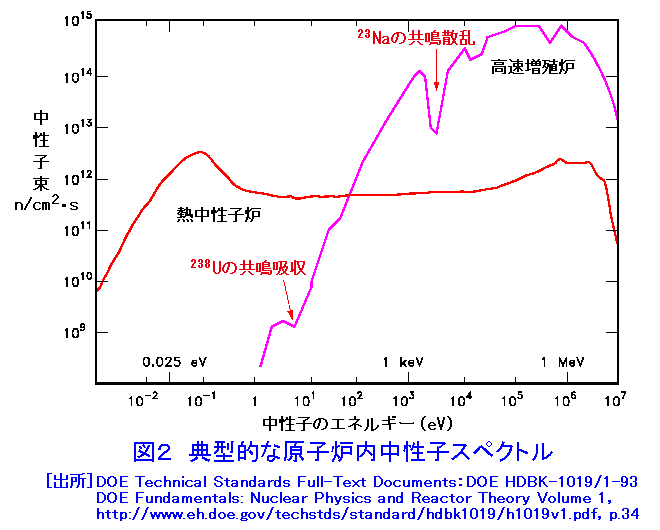
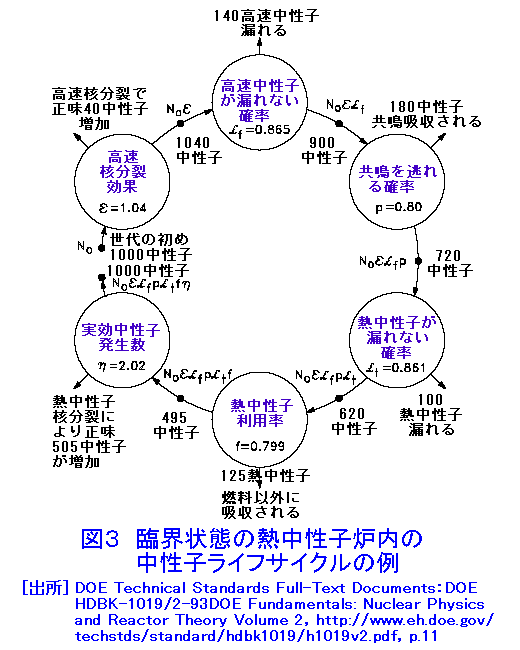
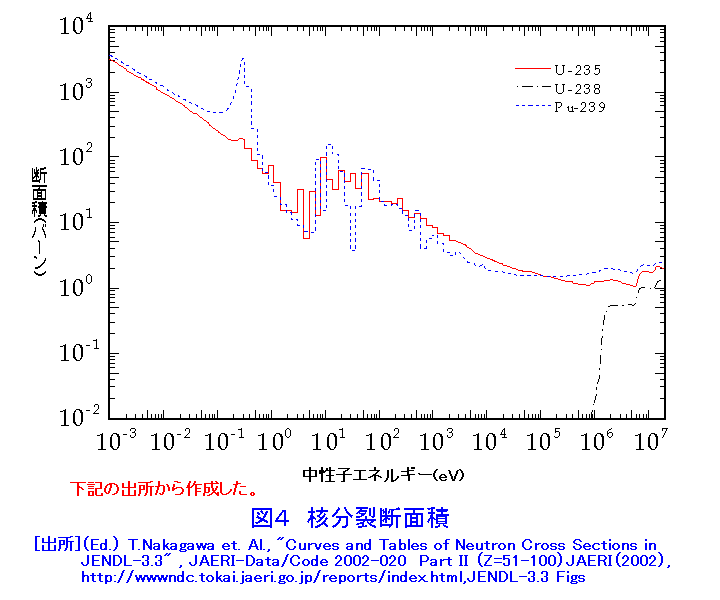
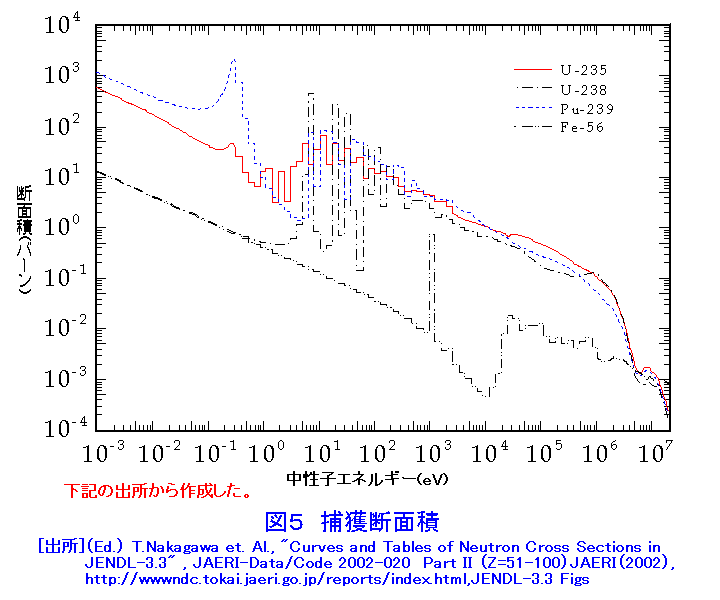
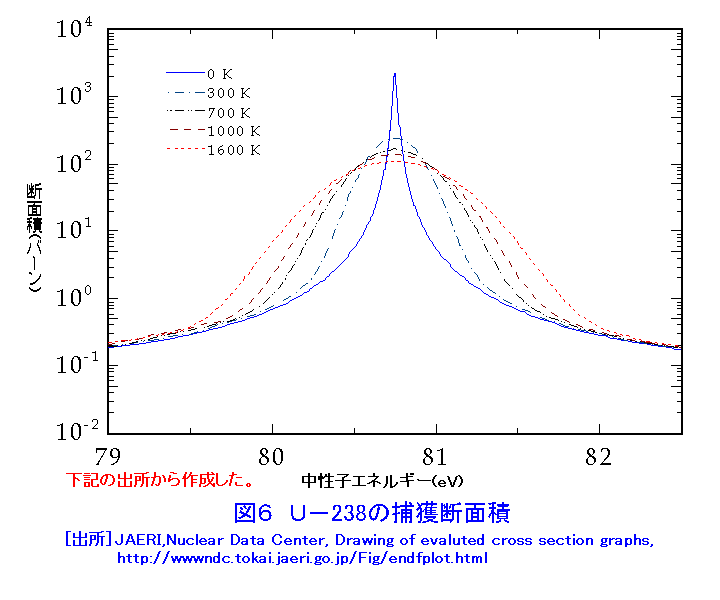
１．原子炉の核設計
（1）核設計の役割
　原子炉の開発では、核設計が重要な役割を演じる。原子炉の安全運転には、原子炉の特性の把握が重要で、精度の高い核設計が必要である。原子炉の改良、新規原子炉の開発に、核設計は不可欠のステップである。核設計は、大きく分けて三段階で、原子炉とかかわってくる。第一段階は核設計による原子炉の特性決定、第二段階は原子炉の性能確認、第三段階は原子炉の運転管理である。
　第一段階は、原子炉の基本仕様を決定するために行われる。例えば、日本原子力研究所大洗研究所（現日本原子力研究開発機構）のHTTRを例にとると、核設計システムとして、図１に示すものが使用され、現在のHTTRの基本仕様が決定されている。第二段階は、核設計の手法が妥当かどうか、導出された核特性が正しいかどうかを臨界集合体により確認する。この際、実験条件によっては、核設計による解析が必要となる。HTTRでは中性子束分布、出力分布の検証の他、表１に示す反応度が測定されている。第三段階は、建設終了後、原子炉起動前に行われる各種のデータの確認と運転管理用データ作成のために行われる。核設計の基本は、原子炉の中で起こる中性子の核反応とそれに起因する中性子の振る舞いを定め、臨界条件を求めることである。
２．臨界条件の取り扱い
（1）古典的臨界条件
　原子炉中の中性子の振る舞いは、単位領域中の中性子増加の割合が、中性子の生成、消滅（吸収、漏れ）とバランスするという関係に基づいている。図２は原子炉の典型的な中性子スペクトル（エネルギー分布）を示している。熱中性子炉では中性子スペクトルは熱エネルギー（0.025eV）を中心とする部分と核分裂スペクトル（0.1〜10MeV）部分とその中間部分（減速領域）に分けられる。減速領域では²³⁸Ｕの共鳴吸収（後述）を除いて中性子の吸収は殆ど無いとして、ライフサイクルに分けた取り扱い（図３）によって、所謂、四因子公式による無限増倍率に中性子が漏れない確率を掛けた、実効増倍率による記述が使用された（表２）。現在は、初期の仕様決定で使われる。
（2）最近の臨界条件の取り扱い
　高速中性子炉の場合、及び最近の第四世代原子炉等の場合、一般に中性子は全てのエネルギーで核分裂を起こすから、図３のライフサイクルに分離した扱いはできない。このため、原子炉の中での中性子の生成と消滅の比として臨界条件を表現する。
　原子炉内ｒ点の単位体積中の速さV（エネルギー E）で、Ω方向に向かう中性子密度ｎ（ｒ，E，Ω）に対して、単位時間に通過する中性子の割合はVnで表される。これを中性子束φという。中性子密度が時間的に変化する割合は、単位時間に発生する割合から漏れる割合と吸収される割合を引いたものに等しい。この方程式は、空気等の気体の運動を表す気体分子運動論の一般化された基礎方程式で、輸送現象について正確な予測を与えるボルツマン方程式と呼ばれるもので、中性子束φ（＝V×中性子密度）、飛行方向Ω（角度）を定める方程式となっている（表３）。実際にはこの方程式は、中性子の角度、速度（エネルギー）について離散化して解くか（決定論的手法：拡散近似、モーメント法、マトリックス法等によって）、モンテカルロ法（確率論的手法：シミュレーション）によって解くかの２つの方法があり、最近では取り入れる近似の少ない（実体系を模擬できる３次元形状や連続エネルギーの取り扱いが容易にできる）シミュレーション法が広く利用され、誰でも、容易に核計算ができるようになっている。
３．輸送方程式に現れる諸量
　入力の定数として、原子炉を構成する物質（燃料、減速材、冷却材、構造材等）の核反応の確率、すなわち巨視的断面積—核分裂断面積、吸収断面積（中性子が原子核に吸収される反応、核分裂断面積（n，f）＋捕獲断面積（n，γ））、散乱断面積（弾性、非弾性）−及び核反応後の２次中性子の角度、エネルギー分布、核分裂から出てくる中性子の角度、エネルギー分布、核分裂あたりの中性子放出数等のデータ（表３）が必要となる。
　これらの量は、r点の単位体積中の原子核Ａの個数密度と核反応Ｘの微視断面積−ATOMICA <03-06-01-03> 原子核と核反応に示されている−を用いて求めることができる（表４）。主要な燃料、親物質（後述）の核分裂及び捕獲の微視断面積を図４、図５に示す。
４．中性子拡散方程式による取り扱い
（1）エネルギースケール
　熱中性子炉では主要な核分裂反応が熱エネルギー、0.001〜0.5eVの範囲で起こる。また、核分裂で発生する中性子は0.1〜15MeVの間にある。このエネルギーの範囲を同時に表現するスケールとして自然対数目盛レサジー（Lethargy：u＝ln（Eo／E），Eoは通常10MeV）を使う。通常の核計算では、このスケールでエネルギー領域を等分しエネルギーについて離散化し、r点のエネルギー群ｇ内の中性子束の総和φg（r，Ω）について輸送問題を扱う。
（2）拡散方程式
　原子炉が充分大きく、あまり複雑な構造でない場合、中性子束の角度による違いはそれほど大きくなく、等方に近い、φg（r，Ω）＝φg（r）＋流れ密度、として扱うことができる。方程式を表５に示す。表中のkeffはこの方程式をの固有値、実効増倍率である。
（3）臨界条件
　核分裂による連鎖反応が進行している媒質中で、臨界になるための条件とは、核分裂反応による中性子の生成と、吸収と漏れによる中性子の損失が釣り合う状態を意味する。表５の式で、
　keff＜1.0の場合、核分裂で発生する中性子の数を真の値νより1/keff倍する必要があることを意味し、未臨界状態であり連鎖反応は起こらない。
　keff＝1.0：臨界状態である。連鎖反応は継続し、中性子数は一定数を保持。
　keff＞1.0：超臨界状態で、中性子の損失（吸収と漏洩による）以上に中性子が発生し、臨界事故を引き起こす状態。
　この臨界条件は、表３の中性子輸送方程式にはC＝1/keffとして適用される。
５．核設計システム
　原子炉では、連鎖核分裂反応が持続するよう、核燃料（²³⁵Ｕ、²³⁹Pu等核分裂によるエネルギーの生成、中性子の生成）、核燃料親物質（中性子捕獲による核燃料への転換、²³⁸Ｕは中性子を捕獲した後、２回ベータ崩壊して²³⁹Puになる。）減速材（散乱による中性子エネルギーの低下）、冷却材（核分裂による発生エネルギーの外部取り出し）、構造材（原子炉の炉心構造部分）、を最適な状態で組み合わせて、核的成立性（臨界条件）、安全性の要件を満たすようにする。その際、表２と核反応断面積の知識が役に立つ、代表的な核種の核反応断面積の値を表６に示す。この表では、原子炉設計で重要な核分裂断面積、捕獲断面積について、2200ｍ値、核分裂スペクトル平均、熱中性子スペクトル平均、高速炉スペクトル平均の数値をあげてある。この後、燃料体、炉心、反射体等の仕様を定め、表３または表５に示す中性子の輸送方程式を解いて実効増倍率や中性子束を求め、実効増倍率、出力分布、スペクトルインデクス（核反応率比、スペクトルの状況を表す指標）、転換（増殖）比、等の特性データを評価し、その仕様の核的効果について検討することが核設計である。
（1）共鳴断面積及び中性子スペクトル変動の効果
　仮に、20種類の原子核が原子炉の燃料集合体、構造材、冷却材として関係があるとすると、核反応の種類を最小４とし70群の扱いをするとして、核計算には5600の微視断面積類が必要になる。散乱については、弾性散乱、非弾性散乱について、g'群からg群への散乱のマトリックスが必要になる。また、Fe、²³⁸Ｕ等の原子核では、あるエネルギーで急激に断面積が増加する中性子の共鳴捕獲がある。図６に²³⁸Ｕの共鳴捕獲を示す。媒質の温度によってドップラー効果によって断面積のピークは減少し、横に広がる。炉内の中性子のスペクトルは中性子が吸収されるため共鳴エネルギー付近で凹みをもち、²³⁸Ｕが多くなるほど凹みは大きくなり、²³⁸Ｕの炉内中性子スペクトルによる平均断面積は小さくなる。これを自己遮蔽効果という。一方、媒質の温度が上昇すると断面積は広がり、スペクトルの凹みは小さくなり、断面積の平均値は大きくなる。高速中性子炉などのスペクトルの硬い炉では、中性子の微視断面積が、統計的にしか判っていない共鳴エネルギー領域が主要なエネルギー領域になる。このエネルギー域の、断面積のドップラー効果が重要な寄与をする。また、スペクトルの硬い炉では、減速の効果を持つ媒質（水素、ナトリウム）の密度が部分的に減少することによって一部でスペクトルがより硬くなり、正の反応度を印加することがある（ナトリウムボイド効果）。これらの扱いも含めた、微視断面積を用意する必要がある。
（2）原子炉計算コードと断面積ライブラリー
・実際の原子炉の設計計算では必要な核反応データを入力定数として、中性子の輸送方程式や拡散方程式を解く計算コードが準備され、比較的容易に利用できる。高度情報科学技術研究機構（RIST）の原子力コードセンター（http://www.rist.or.jp/nucis/）から、これら核定数や原子炉計算コードを入手できる。
・核分裂炉の炉心設計、遮蔽設計、核燃料施設の遮蔽設計、核融合炉のブランケット設計、加速器施設設計などの、幅広い設計や新型炉の研究を目的として、微視断面積の評価済み核データファイルが世界各国で作成され、利用に供されている。米国からは、ENDF/B-VI.8が、日本では日本原子力研究所（現日本原子力研究開発機構）の核データセンターからJENDL-3.3が、ヨーロッパでは、JEFF-3.0が公開されている。これらは原子炉内の中性子輸送計算に使えるよう、中性子エネルギー20MeV以下で起こる全ての有意な核反応のデータを網羅し、汎用ファイルと呼ばれている。
・汎用ファイルは、原子炉の設計計算にすぐに使えるようにはなっていない、炉定数処理コード（NJOY等）を通して、核設計計算を行う輸送計算コード等で利用できる状態に変換して使用する。対象とする炉心等を考慮した中性子束を重みに微視断面積を平均した、エネルギー群数にして数十から数百の決定論コード用の群定数や、特定のモンテカルロ・シミュレーションコード用のライブラリーに変換して使用する。核計算コードとライブラリーとは密に結合しており、通常代表的なライブラリーが、輸送計算コードには組み込んであり、簡単に使用できる。
（3）炉定数（炉計算用の核定数：群定数）中性子エネルギーを多数の群に分割して、そのエネルギー群内では平均された一連の核定数（群定数）が用意されている。多群法に基づく原子炉の解析に必要な群定数は、断面積が媒質の組成、燃料の格子構造（非均質性）、温度など原子炉系で決まる変数に依存する。群定数としては組成、温度、非均質性などはいくつかのパラメータを導入すると自己遮蔽因子などとして理論的に整理でき、炉系に依存しない群定数セットの作成が可能である。通常、これら炉系に独立な一組の群定数を使用して、炉系依存の核反応断面積を作成し、炉心設計、遮蔽設計等の実用計算が行われる。
６．核特性諸量の評価
（1）反応率分布：微視断面積と中性子束から評価される。R（r）＝ ∫σ（e）φ（r，E）dE　その際、測定条件に合わせた核反応断面積作成が重要である。この比は炉内の中性子スペクトルの状態を示す指標となる。
（2）出力分布：出力の平坦化、制御棒の装入位置の決定、熱中性子炉ではキセノン反応度及びこれによる出力振動の抑制で、重要な量である。反応率分布と同様にして求められる。
（3）反応度係数、反応度変化：原子炉の反応度変化には、ドップラー効果に代表される燃料や構造材の温度変化に対し即発的に生じるもの（核的な性質）から、冷却材ボイド効果（高速炉でのNaボイド効果）、減速材、燃料、構造材の温度変化によるの膨張、縮小、変形効果、また、圧力変動による減速材の密度変化等もかかわってくる。これら炉の物理的状況変化に対応した安全上重要なパラメータについては、臨界実験などを用いた核設計値の確認も必要とされる。
（4）毒物による反応度変化：制御棒等の挿入による反応度変化、燃料棒落下等の誤動作による反応度印加、可燃毒物、可溶性毒物等の変動に伴う反応度、出力変動に伴う反応度変化、出力振動などがある。
　その他、動特性パラメータ、燃焼による反応度変化と増殖・消滅処理にかかわる評価等がある。

＜図／表＞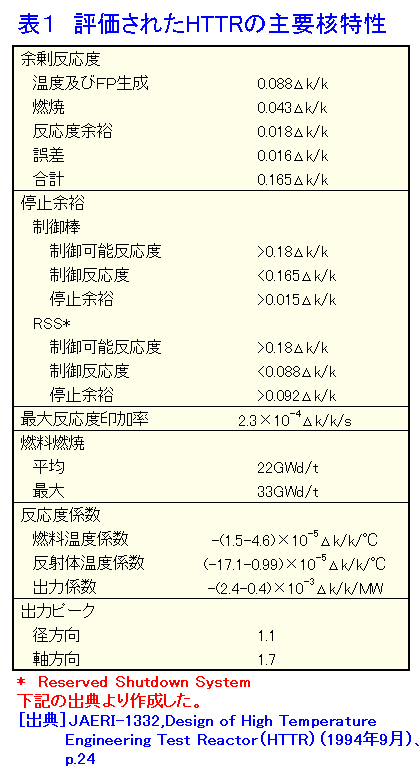

＜参考文献＞
（1）安茂弘（監修）、原子力辞典編集委員会（編）：原子力辞典、日刊工業新聞社（1995）
（2）堀　雅夫（監修）、基礎高速炉工学編集委員会（編）：基礎高速炉工学、日刊工業新聞社（1993）
（3）（Ed.） T.Nakagawa et. Al.， ”Curves and Tables of Neutron Cross Sections in JENDL-3.3 ”，JAERI-Data/Code 2002-020 Part I （Z=1-50） JAERI （2002）
（4）（Ed.） T.Nakagawa et. Al.， ”Curves and Tables of Neutron Cross Sections in JENDL-3.3”，JAERI-Data/Code 2002-020 Part II （Z=51-100）JAERI（2002）
（5）James J. Duderstadt and Louis J. Hamilton ”Nuclear Reactor Analysis” JHON WILEY & SONS，Inc.（1976）（訳本）成田正邦、藤田文行（共訳）：原子炉の理論と解析（上）、（下）、現代工学社（上1980、下1981）
（6） Clefs CEA n°45 − Nuclear physics and safety CEA（2000）
（7）A.M.Weinberg et.al.，The Physical Theory of Neutron Chain Reactors，University of Chicago Press（Oct.1958）
（8）JAERI-1332，Design of High Temperature Engineering Test Reactor（HTTR）（1994年9月）
（9）DOE Technical Standards Full-Text Documents：DOE HDBK-1019/2-93DOE Fundamentals: Nuclear Physics and Reactor Theory Volume 2，
（10）DOE Technical Standards Full-Text Documents：DOE HDBK-1019/1-93DOE Fundamentals: Nuclear Physics and Reactor Theory Volume 1，