|
<解説記事ダウンロード>
<概要>
体系内における中性子(ここでは中性子の集団を問題とするので中性子密度)のふるまいを考える。そのために、まず、中性子のふるまいを理解するのに不可欠な中性子束と中性子流の定義を説明する。次に定義した中性子束のしたがう方程式の導出法と定常状態の中性子の拡散方程式の解法の基本を概説する。中性子束を記述するには時刻\(t\)、位置\(r(=x、y、z)\)、速度\(v(=vx、vy、vz)\)の7つの変数が必要である。このうち\(v\)は\((\frac{1}{2})mv^{2}=E\)の関係で定まるエネルギー\(E\)と、運動方向を表す単位ベクトル\(\Omega(=\theta、\varphi)\)で表すこともある。 <更新年月> 2006年02月 (本データは原則として更新対象外とします。)
<本文>
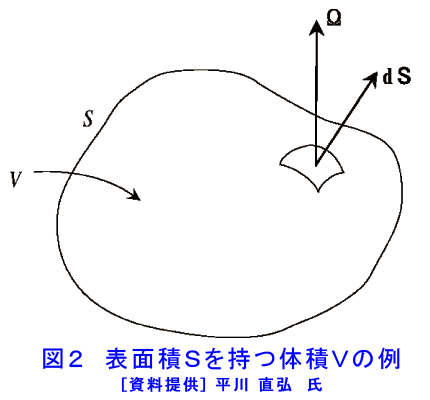
1.中性子束 体系内の中性子のふるまいを明らかにするためには、中性子と体系内の物質の間の反応率を考えなくてはならない。今、すべて同じ速さ\(v(m・s^{-1})\)を持ち中性子密度が\((個・m^{-3})\)である中性子がある方向からミクロ断面積が\(\sigma\)で 原子数密度\(N(個・m^{-3})\)を持つ標的に入ってくるとすると、単位時間にこの標的に入射する中性子数は\(I=nv(個・m^{−2}s^{-1})\)であり、一方この物質のマクロ断面積は\(\Sigma(m^{-1})\)であるから反応率\(R\)は \[ R=\Sigma{n}v(m^{-3}・s^{-1})\tag{1} \] 中性子ビームが1方向でなく、複数の方向からやってくるとすれば、反応率の合計は \[ R=(I1+I2+I3+\dots)\Sigma(m^{-3}・s^{-1}) \tag{2} \] となる。体系内の中性子はあらゆる方向からやってくるので、位置\(r\)にあり、速度ベクトルが\(\Omega\)のまわりの\(d\Omega\)の方向に向いている中性子数密度を\(n(r,\Omega)\)とすると、\(dI(r,\Omega)=n(r,\Omega)vd\Omega\)で与えられる。これによる\(r\)における相互作用率は \[ dR(r,\Omega)d\Omega=\Sigma{n}(r,\Omega)vd\Omega \tag{3} \] 位置\(r\)における相互作用率の総数は \[ R=\int_{4\pi}d\Omega\Sigma{n}(r,\Omega)v=\Sigma\int_{4\pi}d\Omega{n}(r,\Omega)v=\Sigma{n}(r)v\tag{4} \] となる。ここで積分記号にある4\(\pi\)はすべての立体角について積分することを意味する。 \(n(r)=\int_{4\pi}n(r,\Omega)d\Omega\)は\(r\)における単位体積あたりの中性子の総数である。式\((4)\)に現われる中性子密度と速さの積\(n(r)v\)は原子炉物理で基本的な量で、単速の中性子束と呼ばれ、次のように表される。 \[ \varphi(r)=n(r)v\quad(個・m^{-2}・s^{-1}) \tag{5} \] 今考えている中性子のエネルギーを陽に書くと \[ \varphi(r,E,t)=n(r,E,t)v(E) \tag{5'} \] となる。ただし中性子束\(\varphi\)は反応率\(R\)を\(R=\Sigma\varphi\)として計算するために導入された数学的な量であって、ある特定の面積を通過する中性子数と考えるべきではない。 2.中性子流 前節で見たように体系内での中性子の集団としての運動は無数の微分的な中性子ビームの重ね合わせと見ることができる。その微分的なビームはそれぞれ強さが \[ dI(r,\Omega)=n(r,\Omega)vd\Omega \tag{6} \] を持っている。その微分的なビームのうち、強さが\(dI(r,\Omega)\)に等しく、中性子の運動方向\(\Omega\)を向いたベクトルを考える。すなわち \[ dJ(r,\Omega)=n(r,\Omega)vd\Omega \tag{7} \] 中性子流ベクトル\(J\)は\(dJ(r,\Omega)\)をすべての立体角について積分したものとして定義される。 \[ J(r,\Omega)=\int_{4\pi}d\Omega{n}(r,\Omega)v\tag{8} \] \(J\)の物理的な意味を理解するために、たとえば\(J\)の\(x\)成分\(Jx\)を考えてみる。\(yz\)平面上にある単位面積を考え、\(\theta\ x\)を\(v\)という方向と\(x\)軸との間の角度とする。すると\(Jx\)は \[ Jx=\int_{4\pi}n(r,\Omega)v\cos\theta{x}d\Omega\tag{9} \] と書くことができる。\(v\cos\theta\ x\)という量は図1に示すように長さが\(v\)で\(yz\)平面上の単位面積を底面とする傾いた筒の体積である。この体積中にあって、速さが\(v\)で立体角\(d\Omega\)を向いている中性子の個数は\(n(r,\Omega)・v・\cos\theta\ x・d\Omega\)であり、この中性子が単位時間にこの筒の底面を通り抜ける。したがって\((9)\)の積分は、\(x\)軸に垂直な単位面積を単位時間に通り抜ける正味の中性子流を与える。ここで\(Jx\)は\(x\)方向へ向かう正味の数を与えている。というのは、\(yz\)平面を左から右へ通り抜ける中性子数に対しては\(\cos\theta\ x\)が正であり、一方右から左に通り抜ける中性子数に対しては\(\cos\theta\ x\)が負となるので、自動的に差し引きが行われるからである。もし\(Jx\)が正であれば中性子の正味の流れは左から右に向かっている。たとえば、単位面積当り単位時間に\(x\)軸を左から右に3000個、右から左に2000個の中性子が通り抜けていれば、中性子流は\(x\)軸の正方向に単位時間単位面積あたり1000個となる。これに対して\(Jx\)が負であれば正味の中性子の流れは右から左に向かっている。ここでの議論で\(x\)軸の方向は特に指定したものではないので、\(Jx\)の解釈は\(J\)のどの成分についても同様に成り立つ。そこで単位ベクトル\(n\)の方向への\(J\)の成分 \[ Jn=J・n\tag{10} \] が\(n\)に垂直な単位面積を通り抜ける中性子の正味の数を与える。 3.中性子拡散方程式の導出 原子炉体系内に図2のように表面積が\(S\)で任意の体積\(V\)を持つ領域を考える。この領域の中での中性子数の時間的な変化率は、領域\(V\)の中で中性子が発生する率から、領域\(V\)の中で中性子が吸収されたり、逃げ出したりして失われる率を引いたものに等しい。 \(n(r,t)\)を点\(r\)、時刻\(t\)における中性子数密度とすると、領域\(V\)中での中性子数は\(n(r,t\))を体積\(V\)について積分することによって得られる。式\((3.5)\)で定義した中性子束を用いて \[ 中性子変化の時間率 =d\frac{[\int_{V}dVn(r,t)]}{dt}=\int_{V}dV(\frac{1}{v})(\frac{\partial\varphi}{\partial{t}})\tag{11} \] となるので、中性子束の時間変化率は \[ \int_{V}dV\quad(\frac{1}{v})\quad(\frac{\partial\varphi}{\partial{t}})=(V内での発生)-(V内での吸収)-(Vからの洩れ)\tag{12} \] で与えられる。 \(V\)内での発生は\(S(r,t)\)を中性子源の密度とすると \[ (V内での発生)=\int_{V}dVS(r,t) \] \(V\)内の任意の点での吸収反応の時間率は\(\Sigma\ a(r)\varphi(r,t)\)なので \[ (V内での吸収)=\int_{V}dV\Sigma\ a\varphi(r,t) \] となる。 \(V\)からの洩れの率は今考えている領域の表面の点\(rS\)にある\(dS\)という面積を通り抜ける中性子数の時間率が\(J(rS,t)ndS\)であることから(\(n\)は\(dS\)における法線ベクトル)、次のように与えられる。 \[ (洩れの率)=\int_{S}J(rS,t)ndS \] 以上を式\((12)\)に代入し、ガウスの発散定理\((13)\)を用いて表面積分を体積積分に書き換え整理すると、 \[ \int_{S}J(r,t)ndS=\int_{V}\nabla{J}(r,t)dV\tag{13} \] \[ \int_{V}dV[(\frac{1}{v}(\frac{\partial\varphi}{\partial{t}})-S(r,t)+\Sigma_{a}\varphi(r,t)-\nabla{J}(r,t)]=0\tag{14} \] となる。この式は考えている領域\(V\)がいかなる場合にも成り立たなくてはならないので、\([\quad]\)内は恒等的にゼロでなくてはならない。すなわち \[ (\frac{1}{v})(\frac{\partial\varphi}{\partial{t}})=S(r,t)+\Sigma_{a}\varphi(r,t)-\nabla{J}(r,t)\tag{15} \] である。この式は中性子エネルギーがみな同じであるという条件の下では正確な式であるが、\(\varphi(r,t)\)と\(J(r,t)\)という2つの未知関数を含んでいる。そのため\(\varphi\)と\(J\)とを関係付けて、未知数を1つにすることが必要となる。実は\(\varphi\)と\(J\)を関係付ける正確な式はない。しかし、たとえばガスが拡散していくとき、ガス分子が濃度の濃いほうから薄いほうへ、つまりガス密度の濃度勾配に比例して流れていくことが知られている(このような関係は物理の多くの場合に見られる)。そこで\(\varphi\)と\(J\)の間に次のような関係があるとする。 \[ J(r,t)=-D(r)\nabla\varphi(r,t) \tag{16} \] この式をフィックの法則(Fick’s Law)といい、比例定数\(D(r)\)を拡散係数という。 拡散係数は輸送方程式から導かれ、次式で与えられる。 \[ D(r,t)=\frac{1}{3}\Sigma_{tr}=\frac{1}{[3\{\Sigma_{t}−\mu0\Sigma_{s}\}]}\tag{17} \] \(\Sigma_{tr}\)は輸送断面積といわれるもので、ある方向から入射した中性子が散乱を繰り返すうちに入射した方向を忘れるまでに入射方向に対して進んだ距離\(\lambda_{tr}\)の逆数という意味を持つ。また\(\mu0\)は、散乱核の余弦の平均値である。 フィックの法則は(1)体系の境界や孤立して存在する中性子源、強い吸収性の物質など、中性子の強い流れを生む領域から平均自由行程で数倍以上離れている、(2)体系の中性子吸収が小さい、(3)中性子流の時間変化率が中性子と原子核間の核反応の時間に比べて小さい、等の条件の下で成り立つ。式\((16)\)を式\((15)\)に代入すると \[ (\frac{1}{v})(\frac{\partial\varphi}{\partial{t}})=\nabla{D}(r)\nabla\varphi(r,t)-\Sigma_{a}\varphi(r,t)+S(r,t)\tag{18} \] となる。この式を1群(単速)中性子拡散方程式といい、この式を解くことにより体系内における中性子束のふるまいを知ることができる。 4.定常状態における中性子拡散方程式の解法 中性子束に時間変化のない場合を考える。このとき、中性子拡散方程式は \[ \nabla{D}\nabla\varphi(r)-\Sigma_{a}\varphi(r)+S(r)=0\tag{19} \] となる。もし\(D\)が空間的に変化していなければ \[ -D\nabla^{2}\varphi(r)+\Sigma_{a}\varphi(r)=-S(r)\tag{19'} \] である。この形の方程式をヘルムホルツ(Helmholtz)方程式といい、物理数学にしばしば現れる方程式である。またこの式の両辺を\(D\)で割って \[ \nabla^{2}\varphi(r)-(\frac{1}{L^{2}})\varphi(r)=-(\frac{1}{D})\varphi(r) \tag{20} \] と書く。ただし、 \[ L^{2}=\sqrt{(\frac{D}{Σ_{a}})} \tag{21} \] ここに現われた\(L\)は拡散距離と呼ばれ、中性子源を出た中性子が吸収されるまでに進む距離の目安を与える。 式中の\(\nabla^{2}\)はラプラシアン(Laplacian)で、体系の形状により \[ 直交座標系:\nabla^{2}=(\frac{\partial^{2}}{\partial{x}^{2}})+(\frac{\partial^{2}}{\partial{y}^{2}})+(\frac{\partial^{2}}{\partial{z}^{2}})\tag{22} \] \[ 円柱座標系:\nabla^{2}=({1}{r})[\{(\frac{\partial}{\partial{r}})r\}(\frac{\partial}{\partial{r}})]+(\frac{\partial^{2}}{\partial{z}^{2}})\tag{23} \] \[ 球座標系:\nabla^{2}=(\frac{1}{r^{2}})[\{(\frac{\partial}{\partial{r}})r^{2}\}(\frac{\partial}{\partial{r}})]\tag{24} \] である。ただし、円柱座標系、球座標系において中性子束の角度依存性はないものとする。 拡散方程式は2階の微分方程式であるから、解を定めるには、2つの境界条件がいる。それらを一般的に表すと次のようになる。 (1)自由表面(外側が真空の境界)\(r_{s}\)において \[ \varphi(r_{s})=0 \] (2)2つの物質A、Bの境界\(r_{s}\)において \[ \varphi\_{A}(r_{s})=\varphi_{B}(r_{s}) \] および \[ J_{A}(r_{s})=J_{B}(r_{s}) \] または \[ -D_{A}\nabla\varphi(r_{s})=-D_{B}\nabla\varphi(r_{s}) \] (3)局所的に存在する特異点を除いて \[ 0<\varphi(r)<\infty \] また、対称の条件から\(J(0)=0\)で境界条件の一つが与えられることもある。ただし、自由表面においては、体系の内側へ入ってくる中性子流\(J^{-rs}=0\)を境界条件としたい。しかし、拡散近似ではこの条件を満たすことができない。このとき輸送理論により、体系表面から\(z_{0}\)だけ外側の点\(r_{s}'=r_{s}+z_{0}\)の点\(\varphi(rs')=0\)とすれば、この境界条件を満たすことが分かっている。この\(z_{0}\)のことを外挿距離という。 平面の場合、 \[ z_{0}=0.7104\lambda_{tr}\tag{25} \] となる。\(\lambda_{tr}\)は式\((17)\)に現れた輸送の平均自由行程である。また、中性子束の角度依存性を1次の項まで取り入れた近似によれば、\(z_{0}=(\frac{2}{3})\lambda_{tr}=2D\)である。 この\(0.6667\lambda_{tr}\)と正確な\(0.7104\lambda_{tr}\)との差はごく小さい(\(\lambda_{tr}\)が1cmだとすると0.04cmに過ぎない)。したがって普通は\(z_{0}=(\frac{2}{3})\lambda_{tr}\)としてよい。 <図/表> 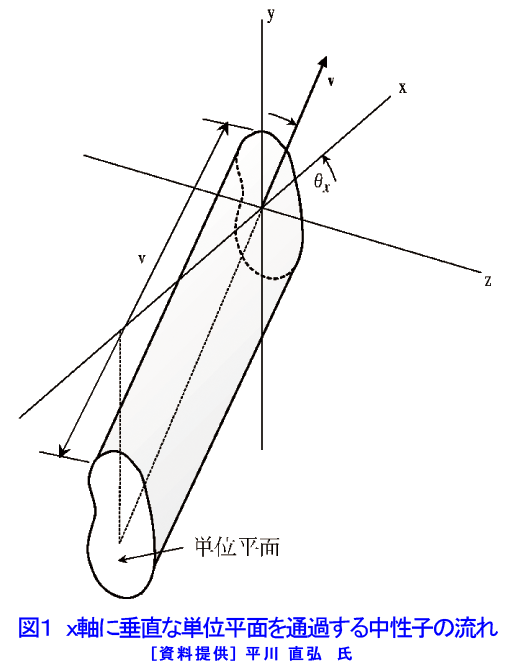
<関連タイトル> 原子核と核反応 (03-06-01-03) 原子炉の炉心核設計概論 (03-06-01-04) 原子炉物理の基礎(1)原子炉の構造と核分裂連鎖反応 (03-06-04-01) 原子炉物理の基礎(2)中性子増倍率と転換、増殖 (03-06-04-02) 原子炉物理の基礎(4)中性子拡散方程式の解法(1) (03-06-04-04) 原子炉物理の基礎(5)中性子拡散方程式の解法(2) (03-06-04-05) <参考文献> (1)平川直弘:原子炉物理入門、東北大学出版会(2003年12月) (2)W.マーシャル(編)、住田健二(監訳):原子炉技術の発展[上]、(株)筑摩書房(1986年9月30日) (3)W.マーシャル(編)、住田健二(監訳):原子炉技術の発展[下]、(株)筑摩書房(1986年10月30日)
|

