|
<解説記事ダウンロード>
<概要>
増倍体系における中性子拡散方程式の解法を検討する。核分裂物質を含む均質な体系における単速拡散方程式を考え、定常状態の場合とした。具体例として、無限平板体系に対する拡散方程式、球形炉心の場合、円柱形の原子炉および反射体付き原子炉、各々について境界条件を定式化し、解法を解説した。 <更新年月> 2006年04月 (本データは原則として更新対象外とします。)
<本文>
増倍体系における中性子拡散方程式の解法を検討する。核分裂物質を含む均質な体系における単速拡散方程式を考える。ここでは定常状態を考えることとする。定常状態とは実効増倍率\(k\)が1であることを意味する。増倍体系では中性子源の項は、\(S(r)=\nu\Sigma_{f}\varphi(r)\) となる。したがってこの場合拡散方程式は \[ \nabla^{2}\varphi(r)-(\frac{\Sigma_{a}}{D})\varphi(r)+(\frac{\nu\Sigma_{f}}{D})\varphi(r)=0\tag{1-1} \] または \[ \nabla^{2}\varphi(r)+[\frac{(\nu\Sigma_{f}-\Sigma_{a})}{D}]\varphi(r)=0\tag{1-2} \] である。またここで\(\nu\Sigma_{f}>\Sigma_{a}\)でなくてはならない。そうでないと第2項の前の符号が負となり、方程式は非増倍体系に対するものと同じ形になる。(本文中の式の表示については表1−1、表1−2を参照) 1.無限平板体系に対する拡散方程式 まず外挿距離を含む厚さが\(a\)の無限に広い平板状体系を考える。 このとき拡散方程式は \[ \frac{d^{2}\varphi(x)}{dx^{2}}+\frac{\nu\Sigma_{f}-\Sigma_{a}}{D}=0\tag{2} \] ここで \[ B^{2}=\frac{(\nu\Sigma_{f}-\Sigma_{a})}{D}=\frac{[(\frac{\nu\Sigma_{f}}{\Sigma_{a}})-1]}{(\frac{D}{\Sigma_{a}})}=\frac{(k_{\infty}-1)}{L^{2}}\tag{3} \] とおくと、 \[ \frac{d^{2}\varphi(x)}{dx^{2}}+B^{2}\varphi(x)=0\tag{4} \] この\(B^{2}\)は原子炉を構成する材料の性質のみによって決まるので、材料バックリングと呼ばれ、これを明確にすることが必要なときには\(B_{m}^{2}\)と表わす。 式\((4)\)の一般解は \[ \varphi(x)=A\cos{Bx}+C\sin{Bx}\tag{5} \] である。 体系が対称、すなわち\(\varphi(x)=\varphi(-x)\)となるときは式\((5)\)で\(C=0\)となるので \[ \varphi(x)=A\cos{Bx}\tag{6} \] となる。 境界条件は外挿境界で\(\varphi(\frac{\pm{a}}{2})=0\)である。 これは \[ B^{2}=\frac{n\pi}{a}\quad(n=1,3,5,\dots)\tag{7} \] に対して満足される。すなわち方程式\((6)\)に対して \[ \varphi_{n}(x)=A_{n}\cos(\frac{n\pi}{a})\quad{n}=1,3,5,\dots \] という無限個の解がある。 \(B_{1}=\frac{\pi}{a}、B_{3}=\frac{3\pi}{a}、B_{5}=\frac{5\pi}{a}\dots\)を固有値、それに対応する\(\varphi_{1}、\varphi_{3}、\varphi_{5}\dots\)を固有関数という。 この問題を時間依存拡散方程式から解くと、解が \[ \varphi(x,t)=\sum_{n(odd)}{A}_{n}\cos(B_{n}x)\exp(-\lambda_{n}t)\tag{8} \] で与えられ、十分時間がたつと\(n=1\) に対応する項以外は消えてしまうことが示される。このとき、基本固有値の2乗すなわち\(B_{1}^{2}\)は体系の大きさ\(a\)のみによって決まるので、幾何学的(形状)バックリングと呼ばれ、区別する必要のあるときは\(B_{g}^{2}\)で表わす。 すなわち、 \[ B_{g}^{2}=B_{1}^{2}=(\frac{\pi}{a})^{2}\tag{9} \] そして、中性子束の空間分布は \[ \varphi(x)=A\cos(B_{g}x)=A\cos[(\frac{\pi}{a})x]\tag{10} \] となる。また上の議論から定常状態では \[ B_{g}^{2}=B_{m}^{2}\tag{11} \] であることが分かる。 なお、臨界未満\((k_{\infty}<1)\)であれば\(B_{m}^{2}<\)\(B_{g}^{2}\)、 臨界超過であれば\(B_{m}^{2}>B_{g}^{2}\)となる。 2.球形炉心の場合 球形炉心に対して拡散方程式は \[ (\frac{1}{r^{2}})[\frac{dr^{2}}{dr}][\frac{d\varphi}{dr}]+B^{2}\varphi(r)=0\tag{12} \] であり、この場合も\(\varphi(r)=\frac{u}{r}\)と置くことにより一般解が \[ \varphi(r)=(\frac{1}{r})(A\cos{Br}+C\sin{Br})\tag{13} \] と求められる。境界条件は外挿距離を含む体系の外側境界\(R\)において\(\varphi(R)=0\)である。 もう一つの境界条件は\(r\to0\)において中性子束が有限、すなわち\(\varphi(r)<\infty\)である。この条件から出てくる無限個の\(B_{n}=(\frac{n\pi}{R})(n=1,2,\dots)\)のうち基本固有値のみが許されるので、 \[ B_{g}^{2}=B_{1}^{2}=(\frac{\pi}{R})^{2}\tag{14} \] そして解は、 \[ \varphi(r)=C(\frac{1}{r})\sin(\frac{\pi{r}}{R})\tag{15} \] 臨界条件は\(B_{m}^{2}=B_{g}^{2}\)であるから \[ (\frac{\pi}{R})^{2}=\frac{(\nu\Sigma_{f}-\Sigma_{a})}{D}=\frac{(k_{\infty}-1)}{L^{2}}\tag{16} \] \(k_{\infty}、L^{2}\)が与えられれば、この方程式から臨界半径\(R\)が定まることとなる。なお、係数\(C\)は拡散方程式が線形方程式である(解の定数倍もまた解である)から一意に定めることはできない。通常は原子炉の熱出力\(P(W)\)が原子炉内での核分裂総数に核分裂数から出力\(W\)への換算係数\(w_{f}\)を用いて \[ P=\int_{0}^{R}4\pi{r}^{2}w_{f}\Sigma_{f}\varphi(r)dr\tag{17} \] を用いて定める。 3.円柱形の原子炉 次に原子炉のもっとも普通の形である円柱形の場合を考える。中性子束が\(r\)と\(z\)の関数とすると、この場合のラプラシアンは\(\nabla^{2}=(\frac{1}{r})[\{(\frac{\partial}{\partial\ r})r\}(\frac{\partial}{\partial\ r})]+(\frac{\partial^{2}}{\partial\ z^{2}})\)で示されるので、この場合の中性子束\(\varphi(r,z)\)の満たすべき拡散方程式は \[ -D[(\frac{1}{r})(\frac{\partial}{\partial{r}})r(\frac{\partial\varphi}{\partial{r}})+(\frac{\partial^{2}\varphi}{\partial{z}^{2}})]+\Sigma_{a}\varphi(r,z)=\nu\Sigma_{f}\varphi(r,z)\tag{18} \] 両辺を\(\Sigma_{a}\)で割り、\(L^{2}=\frac{D}{\Sigma}_{a}、k_{\infty}=\frac{\nu\Sigma_{f}}{\Sigma_{a}}\)とし、式\((3)\)により\(B^{2}\)に置き換え、また中性子束\(\varphi(r,z)\)が\(\varphi(r,z)=\rho(r)Z(z)\)と変数分離できるものと仮定すると、 \[ \frac{1}{\rho(r)}[(\frac{\partial^{2}\rho}{\partial{r}^{2}})+(\frac{1}{r})(\frac{\partial\rho}{dr})]+\{\frac{1}{Z(z)}\}(\frac{\partial^{2}Z}{\partial{z}^{2}})+B^{2}=0\tag{19} \] 境界条件は、外挿距離を含む原子炉の半径を\(R\)、高さを\(H\)として \[ \varphi(R,z)=0\quadおよび\quad\varphi(r,\frac{\pm{H}}{2})=0\tag{20} \] である。 上の境界条件のもとに、この偏微分方程式を解き、その最低次の固有関数と固有値とを取ると、 \[ \varphi(r)=AJ_{0}(\frac{2.405r}{R})\cos(\frac{\pi{z}}{H})\tag{21} \] および、 \[ B_{g}^{2}=(\frac{\nu_{0}}{R})^{2}+(\frac{\pi}{H})^{2}=(\frac{2.405}{R})^{2}+(\frac{\pi}{H})^{2}\tag{22} \] となる。 なお、\(\nu_{0}\)はベッセル関数の最初のゼロ点で2.405\(\dots\)である。 4.反射体付き原子炉 原子炉は一般に多領域から成っている。たとえば殆どの原子炉は核燃料を含む炉心の外側に中性子の洩れを減らすための反射体を有する。また炉心内の中性子束分布を平坦化するため、炉心内を多層化し、それぞれの層に異なる組成(たとえば濃縮度)の材料を配置することもある。したがって我々は多領域の問題を扱う必要がある。その最も簡単な例として厚さ\(a\)の無限平板状の原子炉の外側を、厚さ\(b\)(外挿距離を含む)の反射体が囲んでいる場合を考える。炉心を添字\(_{c}\)で、反射体を添字\(_{R}\)で表わすこととする。 この場合臨界状態での中性子束は次の拡散方程式を満たす。 \[ \begin{align} 炉心:\frac{d^{2}\varphi_{c}}{dx^{2}}+B_{c}^{2}\varphi(x)=0\qquad{B}_{c}^{2}=\frac{(\nu\Sigma_{fc}-\Sigma_{ac})}{D_{c}}\qquad&0<|x|<\frac{a}{2}\tag{23}\\ &(<は等号を含む) \end{align} \] \[ 反射体:\frac{d^{2}\varphi_{R}}{dx^{2}}-(\frac{1}{L_{R}^{2}})\varphi(r)=0\qquad L_{R}^{2}=\frac{D_{R}}{\Sigma_{aR}}\qquad\quad\frac{a}{2}<|x|<(\frac{a}{2})+b\qquad\tag{24} \] 体系は\(x=0\)に対し対称であるから\(x>0\)の領域のみを考えると、境界条件は \[ (a)\quad\varphi_{c}(\frac{a}{2})=\varphi_{R}(\frac{a}{2})\tag{25} \] \[ (b)\quad{J}_{c}(\frac{a}{2})=J_{R}(\frac{a}{2})\tag{26} \] \[ (c)\quad{J}_{c}(0)=0\qquad中心面に関し対称の条件\tag{27} \] \[ (d)\quad\varphi_{R}(\frac{a}{2}+b)=0\tag{28} \] この場合解は、臨界となる炉心および反射体の組成と寸法のある組み合わせに対してのみ存在する。炉心、反射体それぞれの一般解に境界条件\((c)\)、\((d)\)、さらに境界条件\((a)\)、\((b)\)を用いると、 \[ D_{c}B_{c}\tanh(\frac{B_{c}a}{2})=(\frac{D_{R}}{L_{R}})\coth(\frac{b}{L_{R}})\tag{29} \] が得られる。この式が原子炉を臨界とするために、原子炉の組成から決まる量\(D_{c}\)、\(B_{c}\)、\(D_{R}\)、\(L_{R}\)と、原子炉の寸法\((a,b)\)との関係を示している。すなわち式\((29)\)が反射体付き原子炉に対する臨界条件である。 反射体をつけると裸の場合の原子炉の厚さ\(a\)(裸)に比べて原子炉の厚さが少し小さくなる。すなわち、式\((29)\)で\(b=0\)とすると左辺は無限大となるから\(\frac{B_{c}a}{2}=\frac{\pi}{2}\)、つまり、\(a=\frac{\pi}{B_{c}}\)であるが、\(b\neq0\)とすると\(a<\frac{\pi}{B_{c}}\)となる。 裸の原子炉と反射体付き原子炉の厚さの差の\(\frac{1}{2}\)を反射体節約\(\delta\)といい、次式で定義される。 \[ \delta=\frac{[a(裸)-a(反射体付き)]}{2}\tag{30} \] これを臨界方程式\((29)\)に代入し、\(a(裸)=\frac{\pi}{B_{c}}\)を用いることにより、\(\delta\)を与える式が \[ \tan(B_{c}\delta)=(\frac{D_{c}B_{c}L_{R}}{D_{R}})\tanh(\frac{b}{L_{R}})\tag{31} \] と求められる。これより、非常に小型の炉の場合を除くと、(\(B_{c}\)が小さいから)\(\tan(B_{c}\delta)\)〜\(B_{c}\delta\)として良く、 \[ \delta=(\frac{D_{c}L_{R}}{D_{R}})\tanh(\frac{b}{L_{R}})\tag{32} \] 反射体の薄い場合、\(\tanh(\frac{b}{L_{R}})〜\frac{b}{L_{R}}\)となり、\(\delta\ 〜(\frac{D_{c}}{D_{R}})b\)となって、反射体節約が反射体の厚さに比例する。一方反射体の厚さが厚ければ、\(\tanh(\frac{b}{L_{R}})〜1\)とできるので\(\delta\ 〜(\frac{D_{c}}{D_{R}})L_{R}\)という一定値になり、これが最大の反射体節約を与える。ただし、実際には体系から反射体に洩れた高速中性子が反射体内で減速熱化されるため、図1に示すように反射体がある程度以上厚ければ熱中性子束が反射体内でピークを作る。しかしこのことは単速中性子の取り扱いでは説明することができない。 <図/表> 

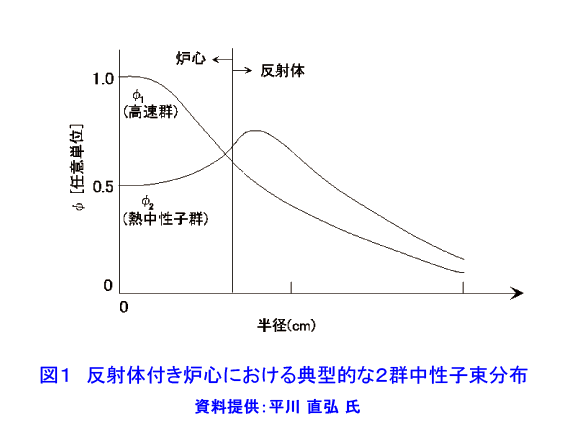
<関連タイトル> 原子核と核反応 (03-06-01-03) 原子炉の炉心核設計概論 (03-06-01-04) 原子炉物理の基礎(1)原子炉の構造と核分裂連鎖反応 (03-06-04-01) 原子炉物理の基礎(2)中性子増倍率と転換、増殖 (03-06-04-02) 原子炉物理の基礎(3)中性子のふるまいと拡散方程式の導出 (03-06-04-03) 原子炉物理の基礎(4)中性子拡散方程式の解法(1) (03-06-04-04) <参考文献> (1)平川直弘、岩崎智彦:原子炉物理入門、東北大学出版会(2003年11月)
|

