|
<解説記事ダウンロード>
<概要>
中性子源を核分裂中性子源と外部中性子源とに区別し、定常状態におけるエネルギー依存中性子拡散方程式を検討する。さらに、多群拡散方程式、1群拡散方程式、2群理論(高速中性子群および熱中性子群)6因子公式等を取り扱う。 <更新年月> 2006年05月 (本データは原則として更新対象外とします。)
<本文>
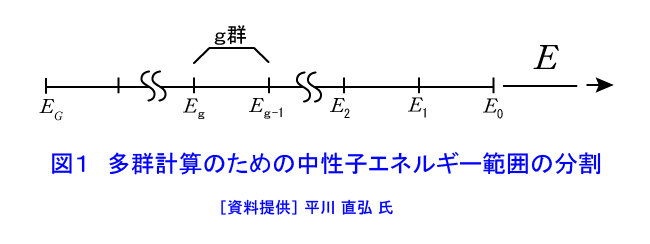
1.エネルギー依存拡散方程式 中性子がみな同じエネルギーを持っているとした場合(単速近似)の空間分布と体系が無限に広いとした場合のエネルギー分布(原子力百科事典 <03-06-04-06>、<03-06-04-07>等参照)を一般化して有限な原子炉体系に対して成り立つ方程式を考える。ここでは中性子源を核分裂中性子源と外部中性子源とに区別して扱う。また定常状態を考える。この場合の方程式は次式となる。(本文中の式の表示については表1−1および表1−2参照) \[ \begin{align} -\nabla{D}\nabla\varphi(r,E)+\Sigma_{t}(E)\varphi(E)=&\int_{0}^{\infty}\Sigma_{s}(E'\to{E})\varphi(r,E')dE'\\ &+\chi(E)\int_{0}^{\infty}ν(E')\Sigma_{f}(E')\varphi(r,E')dE'\\ &+S_{ext}(r,E)\tag{1} \end{align} \] ここでエネルギー範囲は、断面積や中性子束がゼロとなる場合を含め0〜\(\infty\)と一般化している。 2.多群拡散方程式 中性子エネルギーを図1のように\(G\)個に分割し、最も高いエネルギー\(E_{0}\)とし、そこから順に\(E1、E2、\dots\)として最も低いエネルギーを\(E_{G}\)とする。\(G\)番目のエネルギー区間\(E_{g−1}>E>E_{g}\)で式\((1)\)を積分する。 \(g\)群の中性子束を \[ \Phi{g}(r)=\int_{Eg}^{Eg-1}\varphi(r,E)dE\tag{2} \] と定義する。また全断面積を \[ \Sigma_{tg}=(\frac{1}{\varphi_{g}})\int_{Eg}^{Eg-1}\Sigma_{t}(E)\varphi(E)dE\tag{3} \] とする。散乱項については、\(g'\)群から\(g\)群への群間遷移断面積を \[ \Sigma_{sg'g}=(\frac{1}{\varphi_{g'}})\int_{Eg}^{Eg-1}\int_{Eg'}^{Eg'-1}\Sigma_{s}(E'\to{E})dE'dE\tag{4} \] で定義する。また、核分裂断面積について \[ ν_{g'}\Sigma_{fg'}=(\frac{1}{\varphi_{g'}})\int_{Eg}^{Eg'-1}ν(E')\Sigma_{f}(E')\varphi(E')dE'\tag{5} \] とし、さらに、 \[ \chi_{g}=\int_{Eg}^{Eg-1}\chi(E)dE\quadただし\int_{0}^{\infty}\chi(E)dE=1とする)\tag{6} \] \[ S_{g}=\int_{Eg}^{Eg-1}S(E)dE\tag{7} \] とする。拡散係数についての定義は一つでないが、中性子束がエネルギーと空間に分離でき、かつ空間分布が各エネルギーについてみな同じであるという仮定の下で \[ D_{g}=(\frac{1}{\varphi_{g}})\int_{Eg}^{Eg-1}D(E)\varphi(E)dE\tag{8} \] \[ \begin{align} -\nabla{D}_{g}\nabla\varphi_{g}(r)+\Sigma_{tg}\varphi_{g}(r)&=\sum_{g'=1}^{G}\Sigma_{sg'g}\varphi_{g'}+\chi_{g}\sum_{g'=1}^{G}v_{g'}\Sigma_{fg'}\varphi_{g}(r)+S_{g}(r)\\ &(g=1,\dots,G)\tag{9} \end{align} \] となる。これを多群拡散方程式といい、今日の原子炉解析の基礎となる方程式である。 また係数となる群毎の断面積等を「群定数」と呼ぶ。ただしこれらを求めるには積分の中の\(\varphi(E)\)を与える必要がある。 なお、原子炉解析では、外部中性子源項を無視し、また中性子の発生と消滅のバランスをとるため、核分裂源の項を実効増倍率\(k\)で割って \[ \begin{align} -\nabla{D}_{g}\nabla\varphi_{g}(r)+\Sigma_{tg}\varphi_{g}(r)&=\sum_{g'=1}^{G}\Sigma_{sg'g}\varphi_{g'}+(\frac{\chi_{g}}{k})\sum_{g'=1}^{G}v_{g'}\Sigma_{fg'}\varphi_{g}(r)\\ &(g=1,\dots,G)\tag{10} \end{align} \] とする。なお、除去断面積\(\Sigma_{r}\)を \[ \Sigma_{r}=\Sigma_{t}-\Sigma_{sgg}(\Sigma_{sgg}は自群への散乱断面積)\tag{11} \] と定義すると、熱群を除けば中性子の上方群への散乱はないから \[ \begin{align} -\nabla{D}_{g}\nabla\varphi_{g}(r)+\Sigma_{rg}\varphi_{g}(r)&=\sum_{g'=1}^{G}\Sigma_{sg'g}\varphi_{g'}+(\frac{\chi_{g}}{k})\sum_{g'=1}^{G}v_{g'}\Sigma_{fg'}\varphi_{g}(r)\\ &(g=1,\dots,G)\tag{12} \end{align} \] となる。 3.1群拡散方程式 多群拡散方程式において、\(E_{0}=\infty、E_{1}=0\)とすると \[ \int_{0}^{\infty}\chi(E)dE=1、\int_{0}^{\infty}\Sigma_{s}(E\to{E'})dE'=\Sigma_{s}(E)\tag{13} \] であるから、方程式は \[-\nabla{D}\nabla\varphi(r)+\Sigma_{a}\varphi(r)=(\frac{1}{k})v\Sigma_{f}\varphi(r)\tag{14} \] となる。Dが空間に依存しないとし、 \[ \nabla^{2}\varphi(r)+B^{2}\varphi(r)=0\tag{15} \] を用いると、\(\frac{D}{\Sigma_{a}}=L^{2}、\frac{ν\Sigma_{f}}{\Sigma_{a}}=k_{\infty}\)という関係を用いて \[ k=\frac{k_{\infty}}{(1+L^{2}B^{2})}=k_{\infty}P_{TNL}\tag{16} \] という1群理論の臨界方程式が導かれる。 4.2群拡散理論 高速中性子群を第1群、熱中性子群を第2群とする。熱中性子群の上限エネルギーは熱中性子による上方散乱が無視できる0.5〜1eVに取る。そして各群の中性子束を \[ \varphi_{1}(r)=\int_{E1}^{\infty}\varphi(r,E)dE、\varphi_{2}(r)=\int_{E2}^{E1}\varphi(r,E)dE\tag{17} \] とする。また核分裂中性子は第1群のみに現れるので、 \[ \chi_{1}=\int_{E1}^{\infty}\chi(E)dE=1、\chi_{2}=\int_{E2}^{E1}\chi(E)dE=0\tag{18} \] 熱中性子からの上方散乱がないため \[ \begin{align} \Sigma_{s22}&=(\frac{1}{\varphi_{2}})\int_{E2}^{E1}\int_{E2}^{E1}\Sigma_{s}(E'\to{E})dE'dE\\ &=(\frac{1}{\varphi_{2}})\int_{E2}^{E1}\Sigma_{s}(E')\varphi(E')dE'\\ &=\Sigma_{s2}\tag{19} \end{align} \] となるので、熱中性子群の除去断面積は \[ \Sigma_{r2}=\Sigma_{t2}-\Sigma_{s22}=\Sigma_{a2}\tag{20} \] となる。これらを用いると2群の拡散方程式は \[ -\nabla{D}_{1}\nabla\varphi_{1}(r)+\Sigma_{r1}\varphi_{1}(r)=(\frac{1}{k})[ν_{1}\Sigma_{f1}\varphi_{1}(r)+ν_{2}\Sigma_{f2}\varphi_{2}(r)]\tag{21-1} \] \[ -\nabla{D}_{2}\nabla\varphi_{2}(r)+\Sigma_{\alpha2}\varphi_{2}(r)=\Sigma_{s12}\varphi_{1}(r)\tag{21-2} \] となる。 5.6因子公式 高速中性子も熱中性子も同じ空間分布を持つとして、\(\nabla^{2}\varphi(r)+B^{2}\varphi(r)=0\)を用い、\(\varphi_{1}(r)=\varphi_{1}\psi(r)、\varphi_{2}=\varphi_{2}\psi(r)\)とすると、式\((21\)-\(1)\)と\((21\)-\(2)\)を次のようにできる。 \[ D_{1}B^{2}\varphi_{1}+\Sigma_{r1}\varphi_{1}=(\frac{1}{k})(ν_{1}\Sigma_{f1}\varphi_{1}+ν_{2}\Sigma_{f2}\varphi_{2})\tag{22-1} \] \[ D_{2}B^{2}\varphi_{2}+\Sigma_{a2}\varphi_{2}=\Sigma_{s12}\varphi_{2}\tag{22-2} \] この方程式が解を持つ条件から次の式が得られる。 \[ [D_{1}B^{2}+\Sigma_{r1}-(\frac{1}{k})ν_{1}\Sigma_{f1}](D_{2}B^{2}+\Sigma_{a2})-(\frac{1}{k})ν_{2}\Sigma_{f2}\Sigma_{s12}=0\tag{23} \] これを増倍率\(k\)について整理し、 \[ \begin{align} &L_{1}^{2}=\frac{D_{1}}{\Sigma_{r1}}、L_{2}^{2}=\frac{D_{2}}{\Sigma_{a2}}\\ &\frac{ν_{2}\Sigma_{f2}}{\Sigma_{a2}}=(\frac{ν_{2}\Sigma_{f2}}{\Sigma_{a2}^{Fuel}})(\frac{\Sigma_{a2}^{Fuel}}{\Sigma_{a2}})=\eta_{2}f_{2}\\ &\frac{\Sigma_{s12}}{\Sigma_{r1}}=\frac{(熱群に減速される高速中性子数)}{(高速群から除去される数)}=p、\\ &k_{1}=\frac{(\frac{ν_{1}\Sigma_{f1}}{\Sigma_{r1}})}{(1+L_{1}^{2}B^{2})}、\\ &k_{2}=\frac{(\frac{\Sigma_{s12}}{\Sigma_{r1}})(\frac{ν_{2}\Sigma_{f2}}{\Sigma_{a2}})}{(1+L_{1}^{2}B^{2})(1+L_{2}^{2}B^{2})}=\frac{p\eta_{2}f_{2}}{(1+L_{1}^{2}B^{2})(1+L_{2}^{2}B^{2})}=p・\eta_{2}f_{2}・P_{FNL}・P_{TNL}\tag{24} \end{align} \] とおくと \[ k=k_{1}+k_{2}=(\frac{1+k_{1}}{k_{2}})k_{2}\equiv\varepsilon{k}_{2}\tag{25} \] となる。ここで\(P_{FNL}=\frac{1}{(1+L_{1}^{2}B^{2})}、P_{TNL}=\frac{1}{(1+L_{2}^{2}B^{2})}\)はそれぞれ高速中性子、熱中性子が洩れない確率である。 また熱中性子炉において核分裂は主に熱中性子領域で起こるので、\((\frac{1+k_{1}}{k_{2}})=\varepsilon\)(高速中性子核分裂因子)とした。これにより次の6因子公式が得られる。 \[ k=\varepsilon{p}・\eta_{2}f_{2}・P_{FNL}・P_{TNL}\tag{26} \] 6.修正1群理論 大型の熱中性子炉では式\((21\)-\(1)\)の洩れの項\(D_{2}\nabla^{2}\varphi_{2}(r)\)を\(\Sigma_{a2}\varphi_{2}(r)\)の項に対して無視できる。式\((21\)-\(1)\)にこの近似を行い、\(\varphi_{2}(r)\)を式\((21\)-\(2)\)に代入すると \[ -D_{1}\nabla^{2}\varphi_{1}(r)+\Sigma_{r1}\varphi_{1}(r)=(\frac{1}{k})[ν_{1}\Sigma_{f1}+v_{2}\Sigma_{f2}(\frac{\Sigma_{s12}}{\Sigma_{a2}})]\varphi_{1}(r)\tag{27} \] となる。これを修正1群拡散方程式という。この式から\(\varphi_{1}(r)\)を求めれば、\(\varphi_{2}(r)\)は\((\frac{\Sigma_{s12}}{\Sigma_{a2}})\varphi_{1}(r)\)として定まる。 式\((27)\)で\(\nabla^{2}\varphi_{1}(r)+B^{2}\varphi_{1}(r)=0\)とし、 また、 \[ k_{\infty}=(\frac{ν_{1}\Sigma_{f1}}{\Sigma_{r1}})+(\frac{ν_{2}\Sigma_{f2}}{\Sigma_{a2}})(\frac{\Sigma_{s12}}{\Sigma_{r1}})\tag{28} \] とおくと、 \[ k=\frac{k_{\infty}}{(1+L_{1}^{2}B^{2})}\tag{29} \] となる。すなわち実効増倍率が熱群の無限増倍率と高速群の拡散面積を用いた中性子の洩れない確率で与えられる。普通はさらに熱中性子の洩れも考慮して、移動面積\(M^{2}\) \[ M^{2}=L_{1}^{2}+L_{2}^{2}=(\frac{D_{1}}{\Sigma_{r1}}+\frac{D_{2}}{\Sigma_{a2}})\tag{30} \] を用いると、 \[ k=\frac{k_{\infty}}{(1+M_{2}B^{2})}\tag{31} \] が得られる。これを修正1群理論の臨界方程式という。 <図/表> 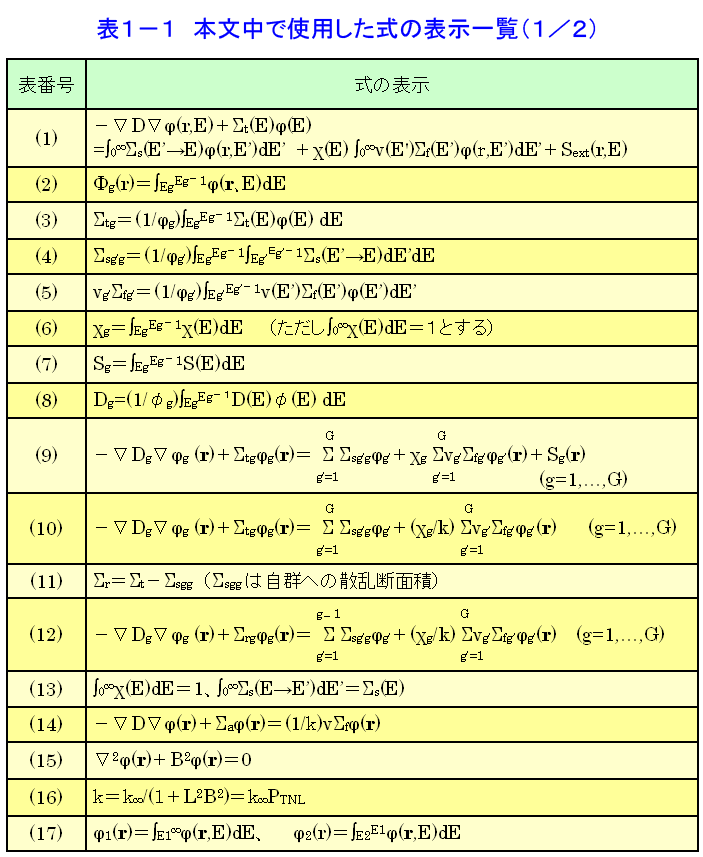

<関連タイトル> 原子核と核反応 (03-06-01-03) 原子炉の炉心核設計概論 (03-06-01-04) 原子炉物理の基礎(1)原子炉の構造と核分裂連鎖反応 (03-06-04-01) 原子炉物理の基礎(2)中性子増倍率と転換、増殖 (03-06-04-02) 原子炉物理の基礎(3)中性子のふるまいと拡散方程式の導出 (03-06-04-03) 原子炉物理の基礎(4)中性子拡散方程式の解法(1) (03-06-04-04) 原子炉物理の基礎(5)中性子拡散方程式の解法(2) (03-06-04-05) 原子炉物理の基礎(6)中性子減速理論 (03-06-04-06) 原子炉物理の基礎(7)種々の体系における中性子の減速 (03-06-04-07) <参考文献> (1)平川直弘、岩崎智彦:原子炉物理入門、東北大学出版会(2003年11月)
|

