|
<解説記事ダウンロード>
<概要>
核分裂連鎖反応を効率良く起こさせるには、中性の散乱反応を利用して、核分裂中性子のエネルギーを下げる(減速する)必要がある。ここでは中性子の減速理論として、弾性散乱による中性子エネルギー損失と散乱角度に関する基本的事項について述べる。 <更新年月> 2006年05月 (本データは原則として更新対象外とします。)
<本文>
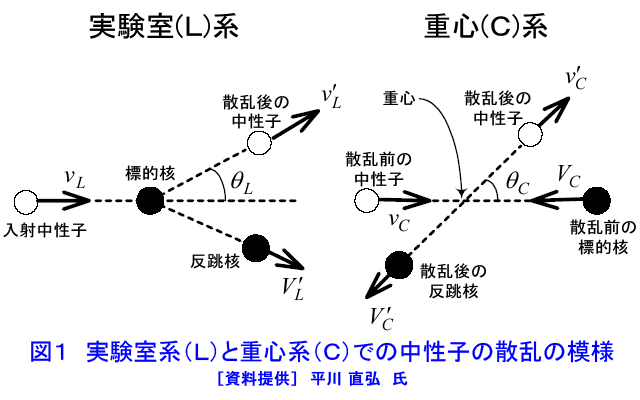
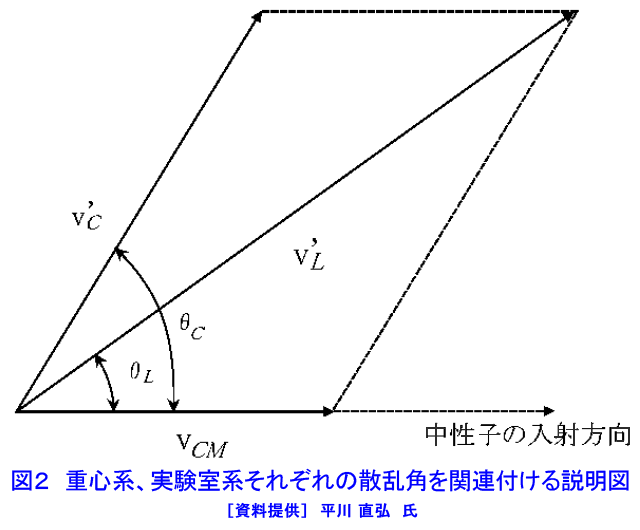
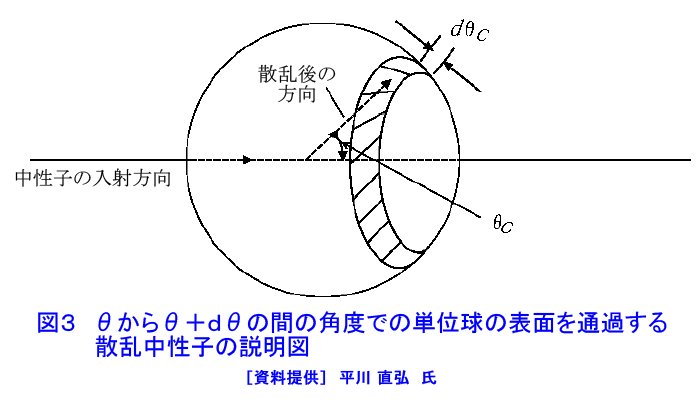
235U等の核燃料物質の断面積は熱エネルギー領域で、核分裂中性子が生まれるMeVエネルギー領域におけるより2桁以上も大きいので、核分裂連鎖反応を効率良く起こすには核分裂中性子のエネルギーを下げる必要がある。中性子のエネルギーを下げるには原子核と中性子の散乱反応を利用する。非弾性散乱では一度に大きなエネルギーを失わせうるが、しきい値があり(238Uでは44keV、12Cでは4.8MeV)、それより高いエネルギーの中性子しか反応を起こさない。したがって原子核との弾性散乱を起こさせることが中性子減速のための唯一の手段となる。(本文中の式の表示については表1参照) 1.弾性散乱による中性子の減速 弾性散乱では、反応前後の運動エネルギーと運動量が保存される。力学的に原子核と中性子の反応を記述する系としては実験室系(我々が通常考える系)と重心系(原子核と中性子の運動の重心に乗った系)の2つがある。運動エネルギーと運動量の保存則が成り立つ反応を記述するには重心系による方が好都合である。そこで、この2つの系の間を関係付ける必要がある。以下、実験室系を\(_{L}\)、重心系を\(_{C}\)という添字で示す。2つの系における反応の様子を図1に示す。中性子の質量を\(m\)、原子核の質量を\(M\)、質量数を\(A\)(〜M/m)とする。以下に実験室系と重心系の間の速さと運動エネルギーの関係を示す。 まず、中性子の速さを実験室系で\(v_{L}\)、重心系で\(v_{C}\)、原子核の速さを実験室系で\(V_{L}\)(今の場合\(V_{L}=0\))、重心系で\(V_{C}\)とし、重心の速さを\(v_{CM}\)とする。重心の速さは \[ (m+M)v_{CM}=mv_{L}+MV_{L}=mv_{L} \] \[ \therefore\quad{v}_{CM}=[\frac{m}{(m+M)}]v_{L}=[\frac{1}{(A+1)}]v_{L}\tag{1} \] となる。この重心の速さを用いると重心系での速さは中性子について \[ v_{C}=v_{L}-v_{CM}=v_{L}-[\frac{1}{(1+A)}]v_{L}=[\frac{A}{(1+A)}]v_{L}\tag{2} \] 原子核について \[ V_{C}=0-v_{CM}=-[\frac{1}{(1+A)}]v_{L}\tag{3} \] となる。上記の速さを用いると、実験室系での全運動エネルギーは \[ E_{L}=(\frac{1}{2})mv_{L}^{2}\tag{4} \] 重心系での全運動エネルギーは \[ E_{C}=(\frac{1}{2})[\frac{Mm}{(M+m)}]v_{L}^{2}\equiv(\frac{1}{2})\mu{v}_{L}^{2}\tag{5} \] ただし、\((\frac{1}{\mu})=(\frac{1}{m})+(\frac{1}{M})\):換算質量で、重心系と実験室系の全運動エネルギーの間の関係は \[ E_{C}=[\frac{A}{(1+A)}]E_{L}\tag{6} \] であることを示すことができる。両者の差、 \(E_{L}-E_{C}=[\frac{1}{(1+A)}]E_{L}\) は、重心自身の運動エネルギーである。 一方、中性子と原子核の運動量の和で与えられる全運動量を実験室系に対して\(p_{L}\)と書くと、 \(p_{L}=mv_{L}\)となるが、重心系での全運動量\(p_{C}\)はゼロとなる。したがって、\(V_{C}=-\frac{v_{C}}{A}\)である。また、運動量保存則により、散乱反応後の全運動量もゼロで、散乱後の量に’をつけて表わすと、 \(V’_{C}=-(\frac{1}{A})v’_{C}\)となる。さらに、重心系でのエネルギー保存則により、 \(v_{C}=v’_{C}、V_{C} =V’_{C}\) となることが示される。すなわち、重心系では、弾性散乱反応の前後で中性子、原子核の速さは変らず、その運動方向のみが変化する。 2.中性子のエネルギー損失と散乱角度 上記の議論から、重心系では弾性散乱によって中性子のエネルギーは変化しないことが分かる。しかし、実験室系では中性子のエネルギーは変化する。この違いを見るには、両者の反応前後の運動方向の変化を取り扱う必要がある。入射方向と散乱後の運動方向の間の角度(散乱角)を実験室系で\(\theta_{L}\)、重心系で\(\theta_{C}\)とする。両者の関係を図2に示す(図中の矢印は運動の大きさとその方向を表わすベクトルである)。これに三角関数の余弦定理をあてはめ、式\((1)\)、式\((2)\)および\(v_{C}=v'_{C}\) の関係を使うと \[ {v'}_{L}^{2}={v'}_{C}^{2}+{v}_{CM}^{2}+2{v'}_{C}v_{CM}\cos\theta_{C}=[\frac{(A^{2}+2A\cos\theta_{C}+1)}{(A+1)^{2}}]v_{L}^{2}\tag{7} \] したがって実験室系における弾性散乱前後の運動エネルギーの比は \[ \frac{{E’}_{L}}{E_{L}}=\frac{{v’}_{L}^{2}}{{v}_{L}^{2}}=[\frac{(A^{2}+2A\cos\theta_{C}+1)}{(A+1)^{2}}]\tag{8} \] この式は、 \[ \alpha=[\frac{(A-1)}{(A+1)}]^{2}\tag{9} \] で定義される\(\alpha\)を用い、あらためて、入射中性子エネルギーを\(E_{i}\)、散乱後のエネルギーを\(E_{f}\)と書くと \[ E_{f}=(\frac{1}{2})[(1+\alpha)+(1-\alpha)\cos\theta_{C}]E_{i}\tag{10} \] と書き直す。この式から \(\theta_{C}=0\) のとき \(E_{f}=E_{i}\) で衝突により中性子はエネルギーを失わない。一方、 \(\theta_{C}=\pi\) のとき、 \[ E_{f}=\alpha{E}_{i}\tag{11} \] で、これが弾性散乱後の中性子エネルギーの最小値である。中性子が弾性散乱で失うエネルギーの最大値を\(\Delta{E}\)と書くと \[ \Delta{E}=E_{i}-E_{f}=(1-\alpha)E_{i}\tag{12} \] となり、最大の損失割合は、 \[ \frac{\Delta{E}}{E_{i}}=1-\alpha\tag{13} \] となる。この式から、エネルギー損失を大きくする(大きく減速させる)には\(\alpha\)の小さい物質(すなわち\(A\)が小さい物質)が有利なことが分かる。特に\(A=1\)(水素)の場合には\(\alpha=0\)、\(\frac{\Delta{E}}{E_{i}}\)=1 となり、1回の弾性散乱でエネルギーがゼロとなり得ることが分かる。 2.1 重心系等方散乱の仮定 式\((8)\)によって中性子のエネルギー変化と重心系での散乱角\(\theta_{C}\)との関係が与えられ、散乱角が分かれば散乱後の中性子のエネルギーが一意的に求められる。しかし、原子炉内では個々の中性子ではなく、中性子全体としての平均的な挙動が重要となる。そのためには、中性子の弾性散乱の角度に関する散乱確率(弾性散乱角度微分断面積)を知る必要がある。中性子のエネルギーが高くなると(数MeV以上)、散乱は強い前方性(散乱角の小さい方へ散乱される確率が高くなる)を持つようになる。しかし、原子炉で問題とするエネルギー領域では、重心系等方散乱、すなわち\(\cos\theta_{C}\)が−1から+1の間の値を等しい確率で取る、という近似が成り立つ。このとき入射中性子エネルギー\(E_{i}\)、弾性散乱後の中性子エネルギー\(E_{f}\)において、 \[ p(E_{i}\to{E}_{f})dE_{f}=-p(\theta_{C})d\theta_{C}\tag{14} \] と書くことができる。この式の左辺\(p(E_{i}\to{E}_{f})\)を散乱確率分布関数という。右辺のマイナス記号は散乱角が大きくなるとエネルギーが減ることを表わしている。式\((8)\)より \[ \frac{dE_{f}}{d\theta_{C}}=-(\frac{1}{2})(1-\alpha)E_{i}\sin\theta_{C}\tag{15} \] また、図3に示される立体角の関係から、重心系で等方散乱された中性子が角度\(\theta_{C}\)の周りの\(d\theta_{C}\)に散乱される確率\(p(\theta_{C})\)は\(p(\theta_{C})=(\frac{1}{2})\sin\theta_{C}d\theta_{C}\) となるので、 \[ p(E_{i}\to{E}_{f})=-p(\theta_{C})[\frac{d\theta_{C}}{dE_{f}}]=\frac{1}{[(1-\alpha)E_{i}]}\tag{16} \] したがって散乱確率分布関数は \[ p(E_{i}\to{E}_{f})=\begin{cases} \frac{1}{(1-\alpha)}E_{i}\qquad&(\alpha{E}_{i}\leqq{E}\leqq{E}_{i})\\[8pt] 0&それ以外 \end{cases} \tag{17} \] となる。すなわち中性子は\(E_{i}\)から\(\alpha{E}_{i}\)までの間のエネルギーに等しい確率で散乱される。 この式を用いて散乱後の中性子の平均エネルギー\(E_{f}\)は \[ E_{f}=\int_{\alpha{E}_{i}}^{E_{i}}E_{f}{p}(E_{i}\to{E}_{f})dE_{f}=[\frac{(1+\alpha)}{2}]E_{i}\tag{18} \] また、衝突ごとに失う平均エネルギー\(\Delta{E}\)は \[ \Delta{E}=E_{f}-E_{i }=[\frac{(1-\alpha)}{2}]E_{i}\tag{19} \] で与えられる。 たとえば水素の場合、\(\alpha=0\)で、中性子は平均して入射エネルギーの\(\frac{1}{2}\)を失う。 2.2 散乱角の平均余弦 次に、散乱反応による平均的な散乱角について考える。実験室系の散乱角\(\theta_{L}\)と重心系における散乱角\(\theta_{C}\)との間の関係は図2、式\((2)\)および\((3)\)から \[ \cos\theta_{L}=\frac{v_{CM}+{v’}_{C}\cos\theta_{C}}{v_{L}}=\frac{1+A\cos\theta_{C}}{\sqrt{(A^{2}+2A\cos\theta_{C}+1)}}\tag{20} \] となる。この式に重心系等方散乱の仮定を用いて、実験室系での散乱角の余弦の平均(平均余弦\(\mu_{0}\))を求めると、 \[ \begin{align} \cos\theta_{C}=\mu_{0} &=\frac{\int_{4\pi}\cos\theta_{L}d\Omega}{\int_{4\pi}d\Omega}\\ &=(\frac{1}{2})\int_{0}^{\pi}\cos\theta_{L}\sin\theta_{C}d\theta_{C}\tag{21} \end{align}\ \] この式の\(\cos\theta_{L}\)に式\((20)\)を代入し、積分を実行すると \[ \cos\theta_{C}=\mu_{0}=\frac{2}{3A}\tag{22} \] が得られる。このことから、ウランのような質量数の大きな核では\(\mu_{0}〜0\)となり、中性子は平均的に90度方向に散乱されるが、\(A=1\)の水素の場合には\(\mu_{0}=\frac{2}{3}\)、すなわち平均として48.2度の方向に散乱される。 <図/表> 
<関連タイトル> 原子核と核反応 (03-06-01-03) 原子炉の炉心核設計概論 (03-06-01-04) 原子炉物理の基礎(1)原子炉の構造と核分裂連鎖反応 (03-06-04-01) 原子炉物理の基礎(2)中性子増倍率と転換、増殖 (03-06-04-02) 原子炉物理の基礎(3)中性子のふるまいと拡散方程式の導出 (03-06-04-03) 原子炉物理の基礎(4)中性子拡散方程式の解法(1) (03-06-04-04) 原子炉物理の基礎(5)中性子拡散方程式の解法(2) (03-06-04-05) <参考文献> (1)平川直弘、岩崎智彦:原子炉物理入門、東北大学出版会(2003年11月)
|

