|
<解説記事ダウンロード>
<概要>
物質は階層構造をなしている。すなわち物質を細かく分割していくと、物質としての性質を変えることなくそれ以上分割できない最小の単位に到達する。これを分子という。分子は殆どの場合複数個の原子(これが元素の最小単位である)からできており、かつてはこれが物質の最終要素と考えられていた。しかし、実は原子は芯になる原子核と、そのまわりを回る電子から構成されている。さらに原子核は陽子と中性子というほぼ同じ質量を持つ2種類の粒子からできている。今日ではそれらがクオークとグルーオンという素粒子からできていることが分かっている。原子炉物理は中性子を介して原子核反応(核分裂反応)を持続的かつ安定的に行わせるとともに、原子核反応の結果生ずる放射線が、反応を起こさせる装置から洩れ出すのを防ぐ方法を見出すことを目的とする分野である。したがって、原子炉物理の理解のためにはまず、原子と原子核についての基本的な知識と、原子核から放出される放射線と物質の相互作用について知ることが必要である。この分野を原子核物理という。 <更新年月> 2006年02月 (本データは原則として更新対象外とします。)
<本文>
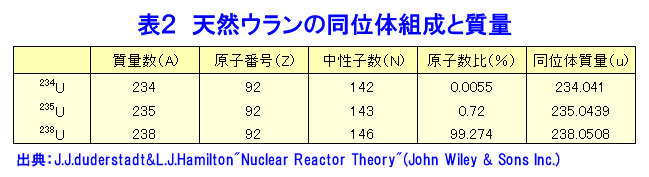
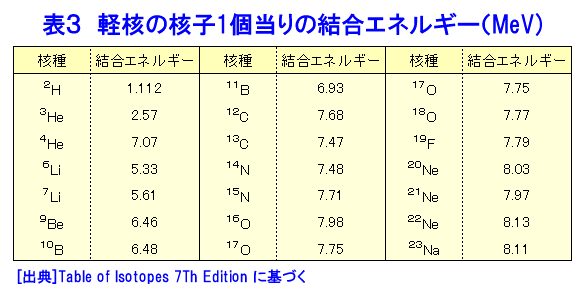
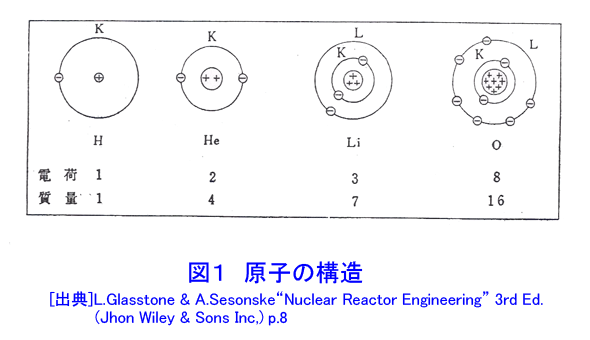
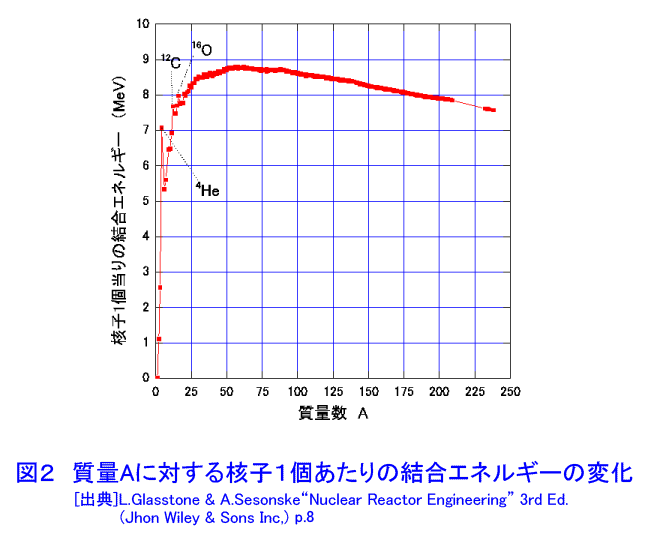
1 原子と原子核 原子は中心に正の電荷を持ち、原子の持つ質量の大部分を占める原子核(以後簡単のため単に核ということもある)のまわりを負の電荷を持つ電子が運動しているという構造をしており、全体としては中性である。核の半径は10-14m程度であるのに対し、電子軌道の拡がりは10-10mの程度である。 核を取りまく電子の数は原子番号Zに等しく、核はちょうどその数に等しいだけの正の電気量+Zeを持つ。ここでeは電子の持つ電荷で−1.602x10-19C(クーロン)である。核は陽子と中性子から成っている。核の中の陽子の数Zと中性子の数Nとの和を質量数といいAで表わす。すなわちA=Z+Nである。陽子と中性子をまとめて核子と呼ぶ。 物質の化学的性質は核を取り巻く軌道電子の数(すなわち核の陽子の数)で決まるので、同じ原子番号の核は化学的には同じように振舞うが、核としては異なる振舞いをする(全く異なることも多い)。そのため、原子核を核内の陽子数と中性子数で分類し、これを核種という。AとZの異なる原子核をひとつひとつ区別して議論するために、通常原子番号Zに対応する原子記号Xにその質量数Aを付記して、表1の(1)と表現する。 Zが同じで質量数Aが異なる(したがってNが異なる)核種を同位体という。たとえば原子炉物理で中心的な役割を占める天然ウランは質量数234、235、238の3つの同位体からなる。これらをそれぞれ、234U、235U、238Uのように表わす。表2に3種の同位体の存在比を示す。 原子の質量は陽子6個、中性子6個、電子6個からなる中性の炭素原子12Cの質量の1/12を単位として、これに相対的に表わす。これを原子質量単位u(atomic mass unit)という。この単位によると、1個の陽子の質量は1.007276u、1個の中性子の質量は1.008665uである。これに対し電子の質量は0.000549uなので、原子の質量はほぼ核内の陽子と中性子の質量の和で与えられる。たとえばもっとも軽い原子である水素原子は陽子1個と電子1個からなり、原子核の質量は1.007276uであるのに対し、電子の質量は0.000549uなので、その比は2000倍近くである。1モルという量は任意の物質の原子量または分子量M(グラム単位)を含む物質の量として定義され、その中に含まれる原子または分子の量は常に6.0225x1023個である。この量をアボガドロ数といい、表1の(2)で表わす。原子質量単位の定義とアボガドロ数を用いると1uは 12/(6.022x1023)x(1/12)x10-3=1.661x10-27kg (1.1) であり、陽子、中性子、電子の質量はそれぞれ 1.673x10-27kg、1.675x10-27kg、9.11x10-3kgと与えられる。 原子構造をはじめて明らかにしたボーア(N.Bohr)の原子模型によると、軌道原子は原子核との間のクーロン力によって決まる特定の軌道上を運動している。そして軌道原子のエネルギーは連続的な値を取れずにある特定の値だけが許される。このことを量子化されたという。軌道電子はクーロン力によって原子核に束縛されているので束縛電子と呼ばれる。 軌道の一番内側の軌道から外の軌道に向かってK軌道、L軌道、M軌道・・と名付けられる。そして軌道に入りうる電子の数はK軌道:2個、L軌道:8個、M軌道:18個のように定まっている。軌道電子のエネルギーはK軌道が一番低く、外の軌道ほど高くなる。したがって電子は一般にK軌道から順に外側の軌道へと空いている場所を埋めて配置される。原子の構造を模式的に図1に示す。 水素原子はK軌道に1個の電子を持ち、HeはK軌道に2個の電子を持つ。LiはK軌道の2個の他にL軌道に1個の電子がはみだしている。また酸素原子はK軌道に2個、L軌道に6個の電子を持つ。エネルギーの一番低い原子の定常状態を基底状態という。原子が電子や外部の原子との衝突によって、あるいは波長の短い電磁波を吸収することによって基底状態からエネルギーの高い状態に移ることを励起されるという。励起状態は一般に寿命が短く(10-8s程度)、電磁波をだして基底状態に戻る。十分大きなエネルギーを吸収して電子が原子核の引力圏外まで出た状態、すなわち原子が電子を失うことを電離という。電離に要するエネルギーを電離エネルギーといい、軌道電子と原子核の結合エネルギーに等しい。 2 粒子性と波動性、エネルギーと質量の等価性 量子力学によると、自然界にあるあらゆる物質は粒子としての性質とともに波としての性質を有している。粒子の運動量をp、プランク定数をhと表わすと、波長λは λ=h/p (2.1) で与えられる。プランク定数は(6.6254±0.0002)x10-344J・sの値を持つ。一方、相対性理論によると粒子も持つ全エネルギーE、静止質量Mo、粒子の運動量pの間に次の関係式がある。 E2=Mo2c4+p2c2 (2.2) cは光の速度で、(2.9979…)x108m/sである。光子(電磁波)の場合、Mo=0であるから光の波長と振動数νの関係式λν=cを用いると E=pc=(h/λ)c=hν (2.3) となる。(2.3)式はアインシュタイン(Einstein)の式と呼ばれ、光の粒子性を表わすものである。電子や中性子のようにM0≠0の場合には E=MC2 (2.4) ただし M=γMo (2.5) ここで γ=1/(1−β2) *ローレンツ(Lorents)因子 (2.6) β=v/c (2.7)の関係がある。(2.4 )はエネルギーと質量の等価性を表わす式である。 (2.2)と(2.5)より p=Moβγc=Mv (2.8) となるから(2.1)より、粒子の波長λは λ=h/Mv (2.9) となる。原子炉物理で扱う粒子のエネルギーは高々10MeV(MeVは次節に説明する電子ボルト)なので、中性子の波長λは電子ボルトで表わした運動エネルギーから次の関係式で求めることができる。 λ=2.86x10-11/(E0.5)(m) (2.10) 3 結合エネルギー 原子核の質量は質量分析計という装置で測ることができるが、その結果、実際の原子核の質量はその原子核を構成する陽子と中性子の質量の和より少し小さいことが分かった。この差を質量欠損ΔMという。今、質量数A、Z個の陽子とN=A−Z個の中性子から構成される原子核の質量をMA、中性原子の質量をM(A,Z)で表わすと、質量欠損ΔMは ΔM=Zmp+(A−Z)mn−MA または ΔM=[Z(mp+me)+(A−Z)mn]−M(A,Z) (3.1) で定義される。ここでmp、mn、meはそれぞれ陽子、中性子、電子の質量である。実際の質量欠損はmp+meを中性の水素原子の質量mH(1.007825u)で置き換えて計算する。すなわち ΔM=ZmH+(A−Z)mn−M(A,Z) (3.2) とする。この質量欠損はZ個の陽子とA-Z個の中性子から原子核を構成するときに解放されるエネルギーと考えることができ、逆に原子核をその構成要素であるZ個の陽子とA-Z個の中性子とにばらばらに分解するときに必要なエネルギーと考えることができる。そこでこの質量欠損に相当するエネルギーを結合エネルギーと呼ぶ。 たとえば水素の同位体である重水素(陽子1個と中性子1個よりなる)の質量は2.014102uなので質量欠損は ΔMD=1.007825+1.008665−2.014102=0.002328 (u) (3.3) となる。 (2.4)よりvという速さで運動している粒子のエネルギーは E=MoC2/(1−β2)=Mc2 (β=v/c) (3.4) で与えられる。原子炉物理の扱う範囲では普通vはcに比べてはるかに小さいので、(2.4)をE=MoC2として計算して良い。したがってm(kg)の質量をJ(ジュール)単位のエネルギーで表わすと、 E(J)=m(kg) x(2.998x108)2=m(kg)x8.988x1016(J) (3.5) となる。1uは1.661x10-2kgなので、 E(J)=m(u)x10-10(J) (3.6) となる。しかし、原子核物理では普通エネルギーの単位としてeVまたはMeVを用いる。1eVというエネルギーの単位は1単位の電荷を1Vの電位差で加速するときに得られるエネルギーとして定義される。1単位の電荷は1.602x10-19C(クーロン)なので1MeVは1.602x10-13Jとなる。したがって E(MeV)=m(u)x931.5 (3.7) となる。すると先ほどの重水素の結合エネルギーは2.22MeVとなる。実際陽子に中性子が吸収されると2.22MeVのガンマ(γ)線が放出され、また重陽子に2.23MeV以上のγ線をあてると陽子または中性子が飛び出してくる。(3.7)から結合エネルギーBEをMeV単位とし、核子1個当りの値として表わすと、 [BE/A= (931.5/A)[1.007825Z+1.008665(A−Z)−M(A,Z)]] (3.8) となる。天然に存在する原子核についてこの核子当りの結合エネルギーを質量数Aについてプロットすると図2のようになる。また、軽い核に対する核子当りの結合エネルギーを表3に示す。BE/Aは質量数の小さいところで質量数とともに急激に増加し(例外的に結合エネルギーの大きい4He、12C、16Oがあるが)、A=60あたりで最大値8.7MeVに達し、以後質量数の増加とともに緩やかに減少しウランのあたりでは7.6MeVとなる(大ざっぱには核子当りの結合エネルギーを8MeVと考えることができる)。 質量数に対するこの結合エネルギーの変化が原子力エネルギーの基本的な原理である。軽い核を結合させてより重い核を作るか(核融合反応)、重い核を分割する(核分裂反応)により、BE/Aがより大きな原子核を作れば大きなエネルギーを得ることができる。たとえば2個の重水素原子を結合させて1個のヘリウム原子(陽子2個と中性子2個からなる)を作ることができれば、 ΔM=2x2.014102−4.002604=0.0256(u) = 23.8(MeV) (3.9) のエネルギーが放出される。また質量数238のウランを分割して2つの質量数119の核を作れば、ウラン238のBE/Aは7.6MeV、A=119付近のBE/Aは8.5MeVなので、(8.5−7.6)=0.9x238=214MeVのエネルギーが解放されることになる。 <図/表> 
<関連タイトル> 原子核物理の基礎(2)原子核の壊変 (03-06-03-02) 原子核物理の基礎(3)核反応 (03-06-03-03) 原子核物理の基礎(4)核分裂反応 (03-06-03-04) 原子核物理の基礎(5)断面積 (03-06-03-05) 原子核物理の基礎(6)放射線と物質の相互作用 (03-06-03-06) 原子核物理の基礎(7)関連用語一覧 (03-06-03-07) <参考文献> (1)平川直弘:原子炉物理入門、東北大学出版会(2003年12月)
|

