原子核物理の基礎（2）原子核の壊変 (03-06-03-02)

＜本文＞
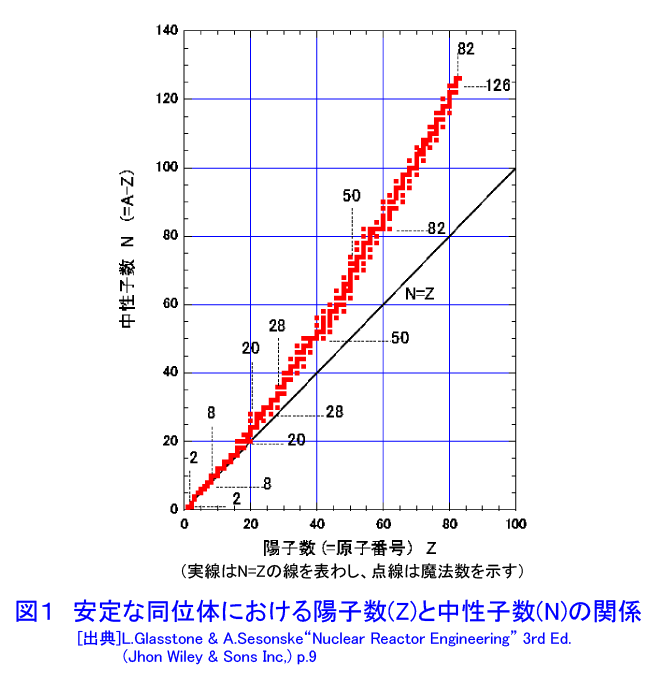
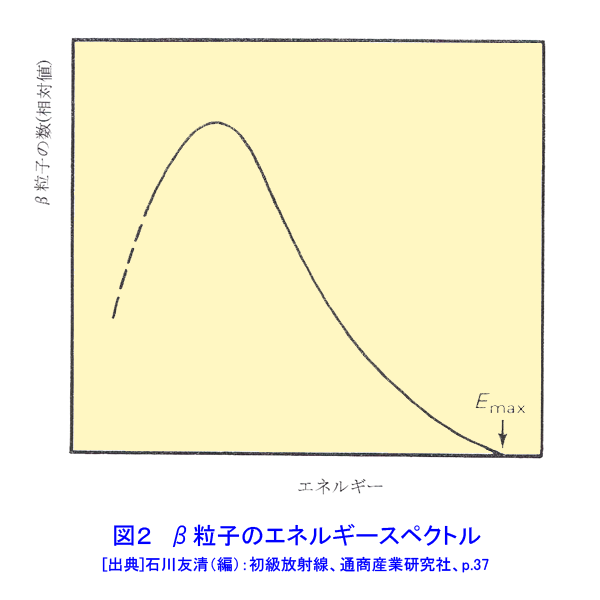
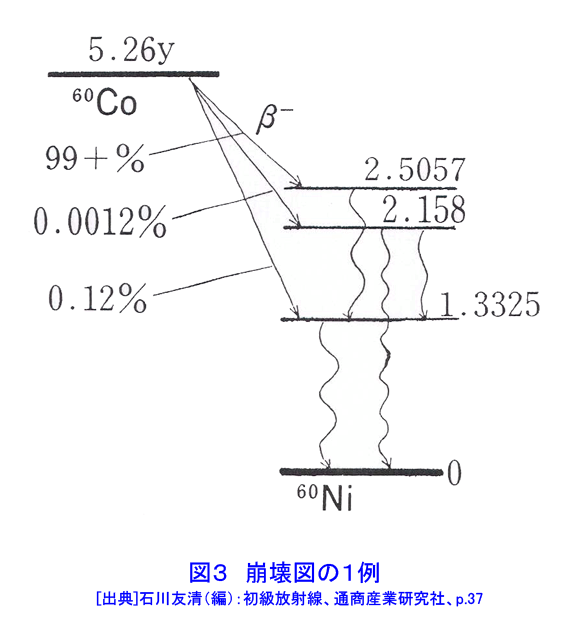
1　原子核の安定性
　原子核は核子がぎっしりと詰まった状態で構成されている、と考えられている。そして原子核の半径は次の式で与えられる。
　　　R＝1.25ｘ10^-15A^1/3（ｍ）　（1.1）
核の中では、主に核子の間でおよそ10^-14ｍ以下の距離でのみ働く核力という近達性の力と、陽子同志で斥力として働くクーロン力の2種類の力が働いている。核力は核内の核子の数に比例し、一方クーロン力は核内の陽子数Ｚの2乗に比例する。また原子核は核内の陽子と中性子が対であるほうが安定であるという性質がある。そのため軽い原子核に見られるように基本的にはＮ/Ｚという比が1に近いものが安定となる。しかしＺが大きくなるとクーロン斥力が大きくなるので、それを核力を増すことで中和する必要があるため、相対的に中性子数Ｎが増すこととなる。この結果質量数が増すとともに安定な核のＮ/Ｚという比は大きくなるが、Ｚ＝84 より上では天然に安定な原子核は存在しなくなる。図１に天然に存在する約270個の核子のＺとＮをプロットしている。核子数が増すにつれてＮ/Ｚの比は大きくなっていき、Ｚ＝82の鉛のあたりでほぼ1.5となっている。ただし、原子核にも原子と同様のシェル構造があり、ＺとＮの数が2，8，20，28，50，82、そしてＮの数が126のところで原子核が特に安定となり、数多くの安定同位体が存在する。たとえばＺが50の錫（Sn）の場合安定な同位体数が10個もある。原子核物理ではこれらの数を魔法の数といい、これらの数の陽子または中性子を持つ核を魔法の核と呼んでいる。また原子核は陽子と中性子の数がともに偶数のときの方が、どちらかが奇数の場合より安定である。陽子、中性子がともに奇数で安定な核は、²H、⁶Li、¹⁰B、¹⁴Nしかない（表１の（1）にＡ，Ｚを並記した記述を参照）。
2　放射性壊変
　安定なＺとＮの組み合わせ以外の原子核は不安定で、核種によって決まっている一定の確率で放射線を出して別の原子核へと壊変していく。α粒子（⁴Heの原子核）を放出する場合（質量数の大きな核に多く見られる）をα崩壊、β⁻粒子（これは電子そのものである）を放出して核内の中性子を陽子に変える場合をβ⁻崩壊という。このとき放出されるα粒子やβ粒子を放射線という。これらは原子番号を使って表１の（2）式のように表わされる。
　ここでνと示したのはニュートリノ（中性微子）と呼ばれる、質量がほとんどゼロの中性の粒子である。（実はニュートリノにはβ⁻壊変に伴うものと陽電子を放出するβ＋壊変に伴うものの2種類があるが、ここでは両者を区別せずに用いる。）
　α壊変でもβ壊変でも原子核をより安定な、よりエネルギーの低い方へと変化させる現象なので、α粒子あるいはβ粒子はそのエネルギーの変化分に相当するエネルギーを持って放出されるはずである。そのため新しくできた原子核が同じであればα粒子やβ粒子の持つエネルギーは一定のはずである。ところがα粒子の場合はエネルギーが一定（線スペクトルを示す）なのに対し、β粒子の場合は図２に示すように最大値を持つ連続スペクトルとなり、平均のエネルギーは最大値のおよそ1/3となる。この差のエネルギーをニュートリノが持って出ると考えられている。
　核内の中性子数が安定な状態より少ない場合には、核内の陽子を中性子に変えて陽電子β^＋（電子と同じ性質を持つ粒子で正に帯電した粒子）を放出するか、あるいは軌道電子を捕獲して陽子を中性子に変える。これを電子捕獲という。この場合、表１の（3）式と表わすことができる。ただし原子炉の運転に伴ってβ^＋壊変を行う核種が生成される例は少ない。γ線は原子核の壊変に伴って生じた核が基底状態へと転移するときに核から放出される光子（電磁波）で、原子核外から放出される光子であるＸ線と区別される。
3　放射能と半減期
3.1　放射性崩壊の指数法則
　天然にある元素のうち、原子番号84のPo（ポロニウム）よりＺの大きい核はすべて不安定であってある決まった割合で放射線を出して壊変していく。またＺ＝81のTl（タリウム）、82のPb（鉛）、83のBi（ビスマス）には安定な核の他に不安定な同位体が存在する。ある放射性核種に対して、その核種が単位時間に崩壊する割合は、その時刻に存在する放射性核種の数に比例する。すなわち、もしＮを時刻ｔに存在する放射性核種の数とすると、壊変率dＮ/dtは
　　　dＮ/dt ＝ −λＮ（3.1）
で与えられる。この比例定数λを壊変定数といい、単位時間の崩壊確率の大きさの尺度である。（3.1）を積分すると、t＝0における放射性核種の数をＮoとして、
　　　ln（Ｎ/Ｎo）＝ −λｔ　（3.2）　　もしくは　 N（t）＝Noexp（−λt）　（3.3）
となる。放射性核種の数が初めの数の1/2になるまでの時間Ｔ_1/2を半減期と呼ぶ。（3.2）の左辺にNo/2を代入すると、
　　　ln（1/2）＝−λＴ_1/2　（3.4）
となるから
　　　Ｔ_1/2＝ln2/λ＝0.693/λ　（3.5）
となる。表２にいくつかの放射性核種の半減期をあげる。このように半減期は100万分の１秒以下のものから数10億年以上までの非常に広い範囲に及ぶ。放射性核種の放射能Ａとは、単位時間に壊変する原子数であって、
　　　Ａ＝−（dＮ/dt）＝λＮ　（3.6）
である。放射能の単位は、毎秒1個の割合で崩壊するとき（1崩壊/秒）、これを1ベックレル（Becquerel）という。
3.2　系列壊変と放射平衡
　たとえば²³⁸Ｕを考えると、²³⁸Ｕはα粒子を放出して234Thとなるが、これは2回のβ⁻壊変を繰り返して²³⁴Ｕとなる（さらに²³⁴Ｕはα粒子を放出して²³⁰Thとなる）。
このような系列を　　λA　　　　 λB　　　　 λC
　　　　　　　　Ａ　　→　　Ｂ　　→　　Ｃ　　→　　Ｄ　→　・・・　→　　Ｘ　　と表わす。このとき、Bという核種の原子数を表わす式は、Bの生成割合が表１の（4）式であるから、表１の（5）式（2.4）　で与えられる。この微分方程式を表１の（6）式（2.4’）　と書き換え、t＝0におけるBの存在数をN_B0として解くと表１の（7）式（2.5）　となる。この場合Ａを親核、Ｂを娘核という。もし親核の半減期が娘核の半減期に比べてはるかに長いとすると、すなわちλ_Aがλ_Bに比べてはるかに小さいとき、表１（8）はｔの大きいところで近似的に表１の（9）式（2.6）　となる。つまり、親核と娘核の存在比が一定となる。これを過渡平衡という。さらにλ_Aは　λ_Bに比べてはるかに小さいことから、表１の（10）とすることができ、　表１の（11）式（2.7）　となる。すなわち、ＢのＡに対する割合が一定であるだけでなく、ＡがＢに壊変していく割合とＢがＣに壊変していく割合が等しくなる。これを永年平衡という。過渡平衡と永年平衡を合わせて放射平衡という。なお、放射性核種の壊変の状況を表わした図を崩壊図という。図３にその例を示す。

＜図／表＞

＜参考文献＞
（1）平川直弘：原子炉物理入門、東北大学出版会（2003年12月）