原子核物理の基礎（6）放射線と物質の相互作用 (03-06-03-06)

＜本文＞
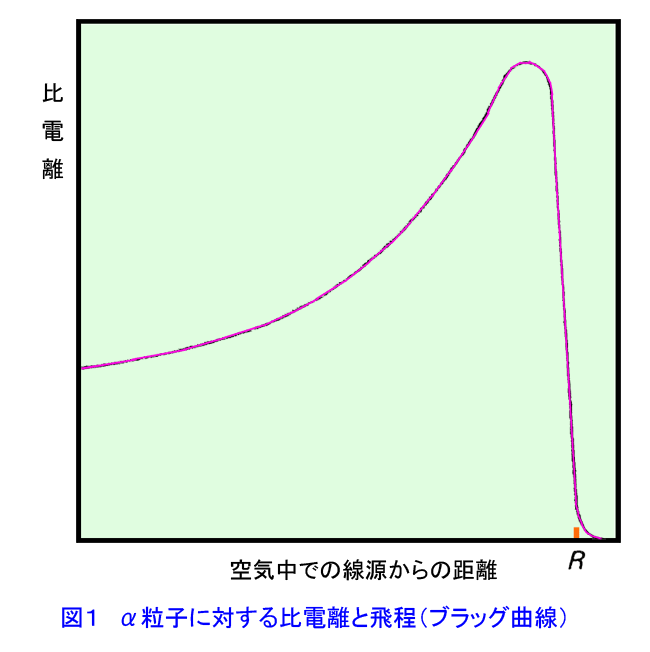
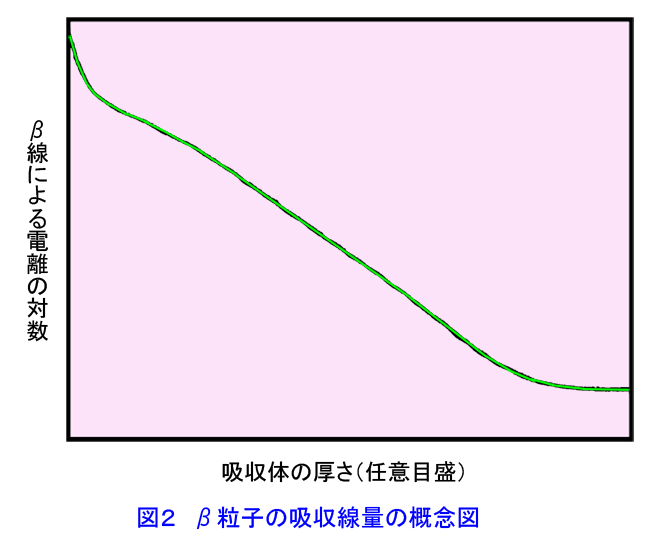
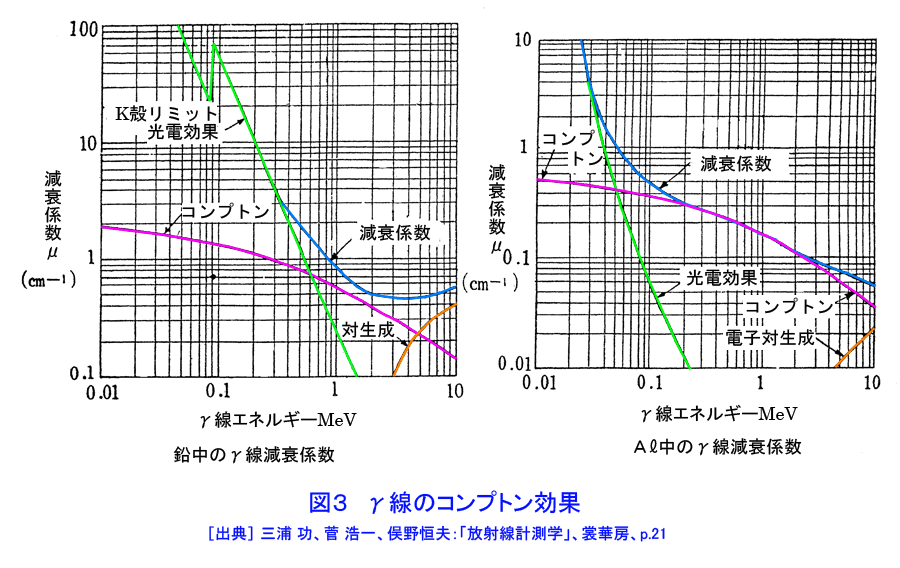
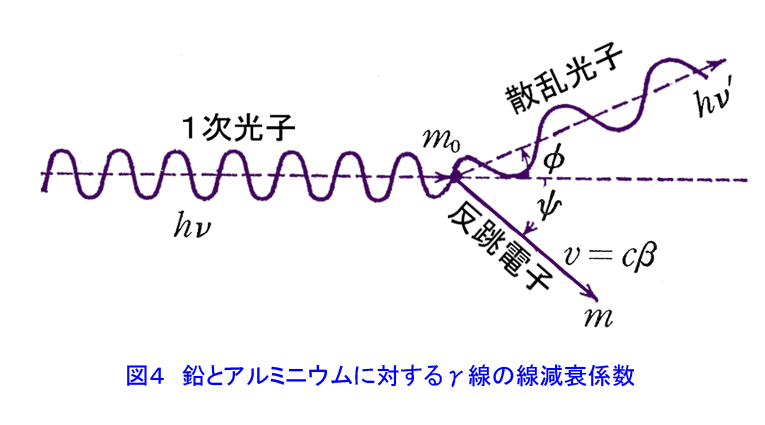
1. 放射線と物質の相互作用
　α粒子やβ粒子のような荷電粒子が物質中を通過すると、物質原子と電気的に相互作用して、原子から軌道電子を剥ぎ取って、その結果電子とイオンとの対を作る。これを電離作用（イオン化）という。大気中では1イオン対を作るのに平均34eV（5.4x10^-18J）のエネルギーが使われる。その結果荷電粒子が通過した物質中に、多くの電子とイオンの対を生ずる。イオン化の強さは、ある物質中を荷電粒子が単位長さ進むときに生ずるイオン対の数で定義され、これを比電離という。同じ質量を持つ荷電粒子の場合、比電離は電荷とともに大きくなる。また同じエネルギーを持つ荷電粒子に対して、質量の大きな粒子の方が（ある原子の近くを通り抜けるのにより長い時間がかかるから）比電離は大きい。たとえば大気圧の空気中で、α粒子は（5〜10）ｘ10⁶個/mのイオン対を作るのに対し、同じエネルギーを持つβ粒子は（3〜30）ｘ10³個/mのイオン対しか作らない。なお、生成されたイオン対は、遅かれ早かれ再結合して熱となって消費される。
1.1　α線と物質の相互作用
　α粒子は電子に比べ非常に重いので、電離作用中にその進行方向を変えることなくα線源から停止するまで直線的に走る。線源からの距離に対しての比電離の大きさを示す曲線をブラッグ（Bragg）曲線という。図１から分かるように、比電離は線源からの距離とともに急速に増加し、終端近くで急激にゼロになる。これはα粒子が物質中を通過する際に、エネルギーを失ってスピードを落とし、その結果物質原子との相互作用の割合が増し、より多くのイオン対を作るようになるからである。これは急激に起こることが分かる。その結果同じエネルギーのα粒子は全てほぼ同じ距離走ったところで停止する。しかしある点を過ぎると、α粒子が物質中の原子の電子を1個、2個と捕らえて最終的に中性のヘリウム原子となり電離作用を失うために終端部で飛跡が長くなっている。全てのα粒子がまったく同じ振舞いを示すわけではないため、カーブは垂直とならずにある傾斜を持つ。これを延長した点（図のＲ）のことを飛程という。空気中の飛程は4.01MeVの²³²Thのα粒子に対し25mm、7.68MeVの²¹²Poのα粒子に対して86mmである。
　空気より密度が大きい物質に対してはその原子密度が大きいため比電離は大きくなる。したがって飛程は空気中におけるより短かくなる。空気中の飛程に対するその物質中での飛程を相対阻止能といい次式で定義する。
相対阻止能＝（空気中でのα粒子の飛程）／（その物質中でのα粒子の飛程）　（1.59）
相対阻止能は水に対して約1000、アルミニウムに対して1600、鉛に対して5000以上である。もし、空気中での飛程が50mmの場合、殆どが水と考えてよい紙や生体中での飛程は50μmとなり、厚さ0.1mmの紙で十分止めることができる。
1.2　β線と物質の相互作用
　ベータ線も荷電粒子なのでα粒子の場合と共通の特徴を持ち、空気中では34eV毎に1対のイオン対を作るが、いくつかの点で違いがある。β粒子は質量が小さいので比電離は同じエネルギーのα線の場合よりはるかに小さい。その結果、飛程はα粒子の場合よりはるかに大きく数〜数10mに及ぶ。またある放射線源からのα粒子は基本的に同一のエネルギーを持つが、β粒子は連続的なエネルギー分布を持つので、α粒子の場合のような決まった飛程を持たない。また直線的に飛ぶα粒子と違ってβ粒子は質量が小さいため、原子核や軌道電子との相互作用の結果、しばしば方向を変える。その結果、同じ厚さの物質中を通過したβ粒子であっても、実際には異なる距離を飛行していることになる。こうした効果が複合する結果、ある放射線源からのβ粒子による電離は距離とともに指数関数的に減少する。その電離の数の対数を吸収体の厚さに対してプロットすると図２のようになる。厚さがきわめて薄い場合と厚い場合を除くと、電離はほぼ直線的に（すなわち指数関数的に）減少している。厚さの厚いところでカーブが水平になっているが、これは制動放射（Bremsstrahlung）という現象による。制動放射とは、高速の電子が物質中を通過するときに原子核の電場による影響を受けて減速され、電磁波（Ｘ線）を出すと同時に方向を変える現象である。この場合のX線のエネルギーは最大がβ粒子の持つ最大エネルギー付近からの連続スペクトルを持つ。その結果厚さの厚いところでは、β粒子は実際にはX線として振舞う。上述したようにβ粒子は決まった飛程を持たないが、あるエネルギーのβ粒子に対して、電離が事実上ゼロとなるのに必要な物質の厚さを定義でき、これを最大飛程という。空気中における種々のエネルギーのβ線の最大飛程を表１に示す。
　β粒子に対する最大飛程はしばしば厚さ密度で表わされる。たとえば0.8〜3MeVの間で、
　　　Rmaxρ（kg/m²）＝5.4Emax−1.5　　　　　　　　　　　　　　　　　（1.60）
この式はアルミニウムに対するものであるが、他の物質に対してもRmaxρはほぼ同じ値を取るとしてよい。たとえば密度2.8ｘ10³kg/m³のコンクリート中での3MeVのβ粒子の最大飛程は
　　　Rmaxρ（kg/m²）＝5.4ｘ3−1.5＝14.7　　　　　　　　　　　　　　　（1.61）
　　　Rmax＝14.7/（2.8ｘ10³）＝5.3ｘ10^-3（m）　　　　　　　　　　　（1.62）
すなわち0.53mmとなる。
1.3　γ線と物質の相互作用
　γ（Ｘ）線は電荷や質量を持たないので、物質中での振舞いはα線やβ線のような荷電粒子の場合と全く異なる。γ線と物質との相互作用には、（a）光電効果、（b）コンプトン効果、（c）電子対生成の3つがある。十分高いエネルギーのγ線は原子核から中性子を叩き出す核反応を起こすこともあるが、原子炉物理の扱う範囲のエネルギーではこの効果は小さいのでここでは考えない。
（a）光電効果
　これは、原子に対する軌道電子の結合エネルギーより大きいエネルギーを持つγ線（光子）が物質に入射すると、軌道電子にその全てのエネルギーを与え、その結果電子が原子から飛び出してくる現象である。飛び出す電子を光電子という。γ線のエネルギーをE、電子の結合エネルギーをBとすると、E−Bが放出される電子の運動エネルギーとなる。光電子の進行方向は、ごく低いエネルギーのγ線の場合を除き、入射γ線の方向と同じである。放出された電子はβ粒子と同じ振舞いをする。
　光電効果の起こる確率は、原子核との結びつきの強い電子ほど大きいので、実際上K電子によって殆ど起こることとなる。光子のエネルギーをE、物質の原子番号をZとすると、光電効果の起こる確率はほぼ
（光電効果の起こる確率）＝（比例定数）ｘ（Zⁿ/E³）　　　　　　　　　　（1.63）
ここでnはエネルギーの低いとき3、エネルギーの高いとき5の程度である。したがって光電効果は吸収物質の原子番号が大きくγ線のエネルギーの小さいときほど大きい、たとえば鉛の場合は500keV以下、アルミニウムの場合は50keV以下で大きな効果を持つ（図３参照）。
（b）コンプトン効果
光子のエネルギーが高くなると軌道電子の束縛エネルギーが無視できるようになり、光子が吸収物質の電子と弾性散乱を起こす。これをコンプトン効果という。このとき、エネルギーと運動量の保存則から（γ線の運動量は非常に小さいため）、電子に移るγ線のエネルギーは入射するγ線のエネルギーの一部であり、散乱されたγ線はもとのγ線より低いエネルギーとなって方向を変える（図４）。入射γ線のエネルギーをE，散乱後のγ線のエネルギーをE’とすると、
　　　E’＝0.51／［1−cosθ＋0.51/E］　（MeV）　　　　　　　　　　　　（1.64）
という関係がある。0.51MeVというのは電子の静止質量である。この式からcosθ≒1であればＥ'≒Eである。すなわち前方散乱（θ≒0）の場合、散乱γ線のエネルギーは入射γ線のエネルギーにほぼ等しい。他方、θ＝90°のとき、
　　　E'＝0.51/［1＋0.51/E］　＜ 0.51 （MeV）　　　　　　　　　　　　（1.65）
となって、90°方向に散乱されたγ線は0.51MeV 以上のエネルギーを持ち得ない。コンプトン散乱は光子と電子との相互作用なので、その確率は吸収物質の軌道電子数すなわち原子番号に比例する。一方コンプトン効果はエネルギーＥに反比例する。すなわち
　　　コンプトン効果の確率 ≒（定数）x（Z/E）　　　　　　　　　　　　（1.66）
コンプトン効果が重要な役割を占めるエネルギー領域は、鉛では0.6〜5MeV、アルミニウムでは0.05〜15MeVである。
なお、これに続く（c）電子対生成、（d）γ線の減衰、（e）中性子と物質の相互作用は、表２に続編の形でまとめた。また、鉛とアルミニウムに対するγ線の線減衰係数を図３に示す。

＜図／表＞

＜参考文献＞
平川直弘、岩崎智彦：「原子炉物理入門」、東北大学出版会（2003年10月）