|
<解説記事ダウンロード>
<概要>
原子炉物理の理解のための前提条件として原子と原子核についての基本的な知識と、原子核から放出される放射線と物質の相互作用について知ることが必要である。この分野を原子核物理と呼んでいるが、本タイトルは原子核物理の基礎としての「原子核の構造」<03-06-03-01>に始まる一連の内容についてシリーズ形式で記述したものであり、シリーズ物が総合されてサブタイトルの「原子核の物理」編として完結する。 <更新年月> 2006年06月 (本データは原則として更新対象外とします。)
<本文>
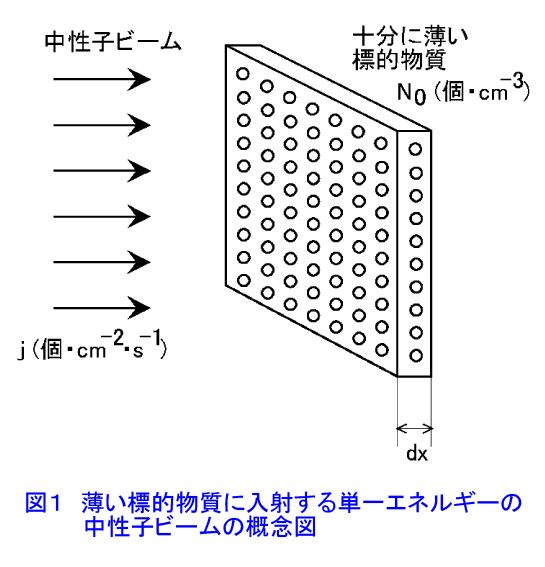
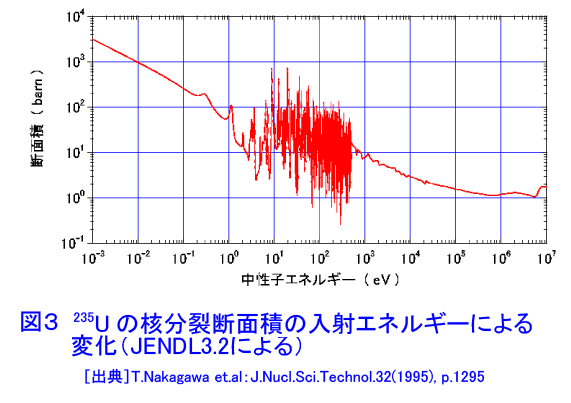
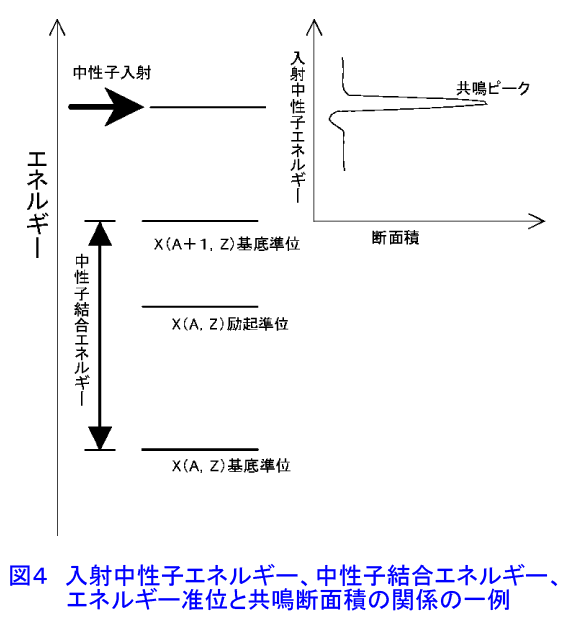
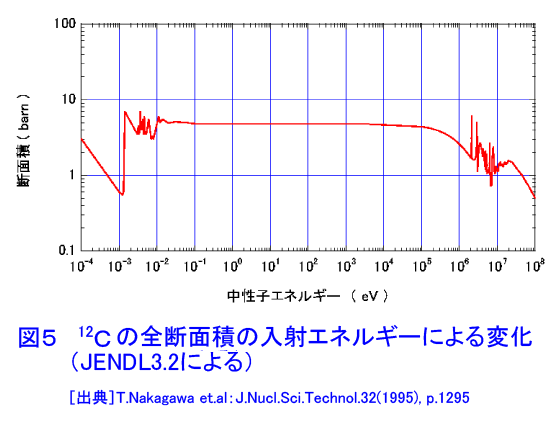
1. 断面積 1.1 ミクロ断面積とマクロ断面積 これより先我々は原子核と中性子の間の反応を定量的に扱わなくてはならない。そのために必要となる、中性子が核と反応する確率に相当する概念「断面積」を導入する。今、図1に示すように単位面積当り毎秒j個の中性子の流れ(個・m-2・s-1)が単位面積当りNo(個・m-3)の原子を含むきわめて薄い標的(厚さdx(m))に垂直に入射しているとする。厚さが薄いということは、入射する中性子が標的の後ろの方にある原子核に達する前に減少してしまわないことを保証するための仮定である。このような状況下での単位時間、単位体積当りの反応率R(個・m-2・s-1)は、入射中性子の流れの強さjと存在する標的核の数(中性子数)Nodx(個)に比例するはずだから、比例定数をσと書くと(本文中の式の表示については表1参照) R=σjNodx または R=σjNA ただしNA=Nodx ・・・(1) となる。これを R/NA 単位時間当り標的核1個当りの反応率 σ=——— = —————————————————— ・・・(2) j 単位時間当り単位面積当りの中性子入射数 と書き直すとσは単位時間単位表面積当りに1個中性子が入射するとき、単位時間にどれだけ数の反応が起こるかを示す量となっていることが分かる。原子炉物理ではσが面積(m2)の単位を持つことからσをミクロ断面積と呼ぶ。そして10-28m2を特別の単位とし、これをバーン(b)と呼んでいる。これは原子核の半径が10-14mの程度なので、その断面の面積は10-28m2程度となることに由来している。 さらに1つの原子核でもいろいろな核反応を起こすことから反応毎にミクロ断面積を定義し、σにそれぞれの反応を示す添字をつけてそれらを区別する。主なものには散乱断面積σs、吸収断面積σa、核分裂断面積σf、捕獲断面積σc(またはσγ)がある。この他、原子炉物理では、全ての反応断面積を総和した全断面積σtがよく現れる。σtはσsとσaの和として与えられる。なお、吸収断面積には核分裂断面積も含むので他の反応のない場合、σa=σf+σcであることに注意して欲しい。ミクロ断面積の大きさは核種によって、また入射中性子のエネルギーによって大きく変化する。核種によっては数100万バーンという大きな断面積をもつこともある。このため断面積の大きさについて、一般的に議論することはできない。 次いで図2のように、標的が単位体積当りNo個の原子を含む厚い板の場合を考え、その表面にjo(個・m-2・s-1)の単一のエネルギーの中性子が垂直に入射している場合を考える。このとき、板の表面からxのところにある微小な厚さdxの部分を考え、ここでの中性子の流れをj(x)と表わすと、厚さxからx+dxの間での中性子の流れの減少−djは、σを全断面積とすると −dj=σj(x)Nodx (マイナスの記号は減少を表わす) ・・・(3) と表わすことができる。この式から −dj/j=σNodx ・・・(4) であるから、これを積分して j(x)=jo exp(−σNox) ・・・(5) となる。σとNoの積をΣと書いてマクロ断面積という。すなわち Σ=σNo ・・・(6) である。他のミクロ断面積についても、上式と同じ形で各反応に対するマクロ断面積が定義される。ただし、Σは断面積という名はついているが、実はデイメンジョンはm-1で面積(m2)の単位ではないことに注意して欲しい。また、(6)よりΣは −dj/j Σ = ———— ・・・(7) dx と書くことができるから、Σは単位長さ当りに中性子の流れが減少する割合を表わしていることが分かる。 1.2 断面積のエネルギー変化 先に述べたように断面積の大きさは核によって大きく変わると同時にエネルギーによっても大きく変化する。ここでは質量数の大きな核(重核)と、質量数の小さな核(軽核)についてミクロ断面積のエネルギー変化を原子炉物理において重要な2つの核235Uと12Cを代表として見ていくこととする。質量数の中位の核(中重核)はおおむねこの両者の中間の変化を示す。 (a)質量数の大きな核 図3に入射中性子エネルギーに対する235Uの核分裂断面積の変化を示す。質量数の大きな核の断面積のエネルギー変化はおおむねこの235Uの場合と同様になる。 1eV以下のエネルギーの低い領域では、断面積は1/v(=1/√E)に比例して減少する。 しかし1eV付近より上では大きな凹凸を繰り返す。これを共鳴といい、中性子のエネルギーが複合核の励起準位と一致したときに核反応が起こりやすくなることを示している(図4参照)。中性子のエネルギーが高くなるにつれて共鳴断面積のピークの高さが次第に小さくなると同時に共鳴のエネルギー幅が拡がって、結果的に滑らかな断面積変化を示すようになる。そして1MeVを超えると核分裂断面積は階段状に上がっていく。 捕獲断面積のエネルギー変化も1MeV以上の高エネルギー領域で単調に減少することを除いては、この核分裂断面積と同様の変化を示す。また核分裂を起こさない核では高エネルギー領域で(n,p)、(n,α)等の荷電粒子放出反応が起こるようになる。 (b)質量数の小さな核 図5に12Cの全断面積のエネルギー変化を示す。12Cの場合、吸収断面積が小さいため、この全断面積=散乱断面積と考えてよい。質量数の小さい核はこの12Cと共通したエネルギー変化を示すことが多いが、全く異なった変化を示す核も少なくない。 図5から分かる通りもっとも低いエネルギー領域(10-4 eV程度)ではほぼ1/vに比例するエネルギー変化を示す。10-3〜10-2 eVの間で断面積が急激に大きくなり、その後不規則なジグザグを示す。これは、このエネルギーで中性子の波長(λ=h/Mv)が炭素原子の原子間距離と同程度となり、中性子が炭素原子核とでなく、炭素原子と相互作用するようになるため、黒鉛の結晶のように物質が規則的な構造を持つとき、中性子が結晶面で回折現象を起こすためである(中性子の波長が結晶の格子面間距離の整数倍となるところで回折を起こす)。 この領域よりエネルギーが高くなると回折は起こらなくなり、核そのものの大きさできまる断面積で反応が起こるようになる。この領域をポテンシャル散乱領域といい、断面積は広いエネルギー範囲にわたり σp=4πR2 (R;原子核半径) ・・・(8) で表わされるポテンシャル散乱断面積を取る。 ポテンシャル散乱領域より上のエネルギー領域(12Cでは1MeV以上)では235Uの場合に見られたのと同様の共鳴散乱が起こる。ただし、散乱断面積の場合、共鳴散乱とポテンシャル散乱の間で干渉が起こるので、共鳴のピークの下側で断面積が小さくなり、上側で大きくなる特徴がある(図4参照)。このことは遮蔽の問題において重要となる。 さらに、この領域より上の領域では、中性子の波長が原子核の大きさに比べて短くなるため、原子核と相互作用する確率が減るので、エネルギーが上がるにつれて断面積が小さくなる。しかし、核分裂連鎖反応に伴う中性子のエネルギーは最大10MeV程度なので、原子炉の解析においては非常に高いエネルギーの中性子の挙動は問題にしなくてよい。 <図/表> 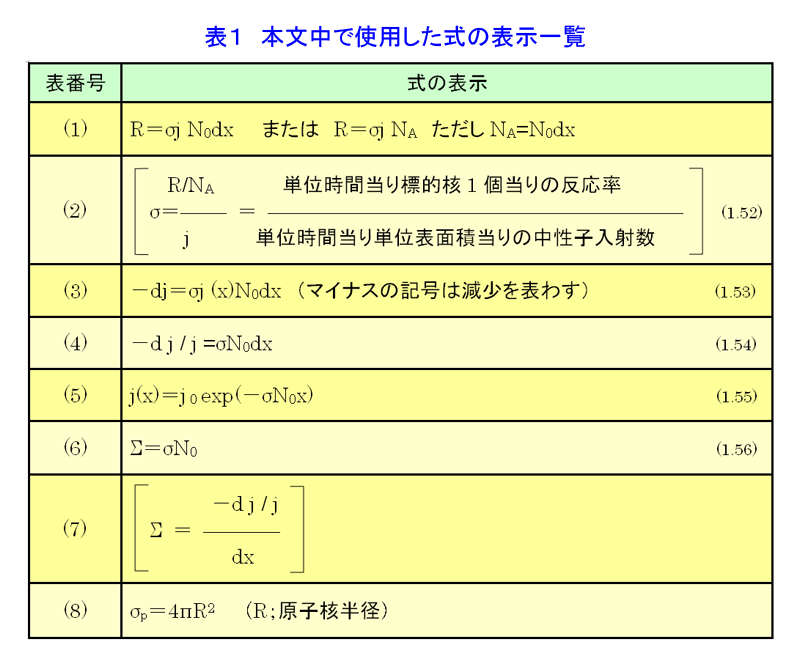

<関連タイトル> 原子核物理の基礎(1)原子核の構造 (03-06-03-01) 原子核物理の基礎(2)原子核の壊変 (03-06-03-02) 原子核物理の基礎(3)核反応 (03-06-03-03) 原子核物理の基礎(4)核分裂反応 (03-06-03-04) 原子核物理の基礎(6)放射線と物質の相互作用 (03-06-03-06) 原子核物理の基礎(7)関連用語一覧 (03-06-03-07) <参考文献> 平川直弘、岩崎智彦「原子炉物理入門」東北大学出版会(2003年10月)
|

