被ばく線量に応じた細胞の反応にかかわる諸モデル (09-02-02-09)

＜本文＞
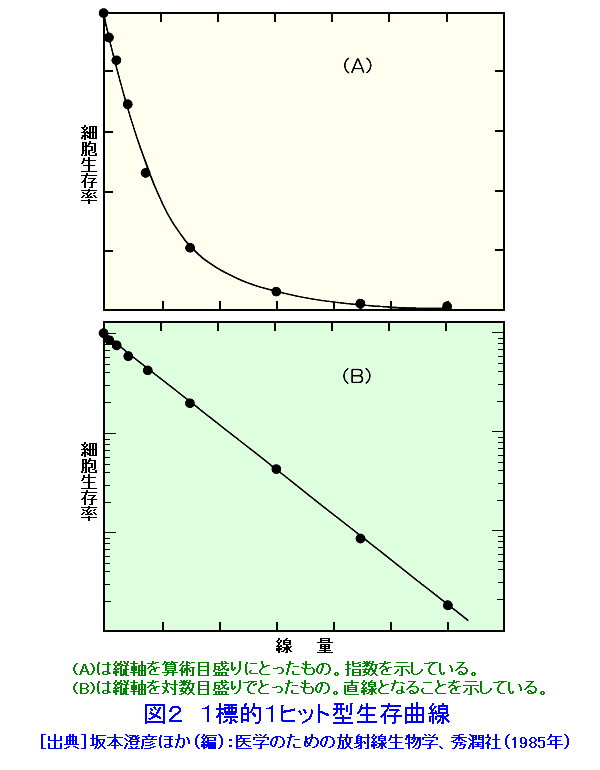
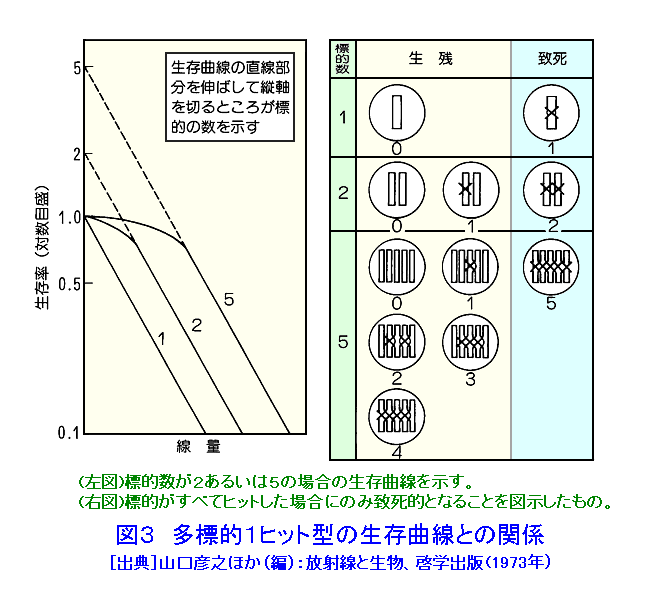
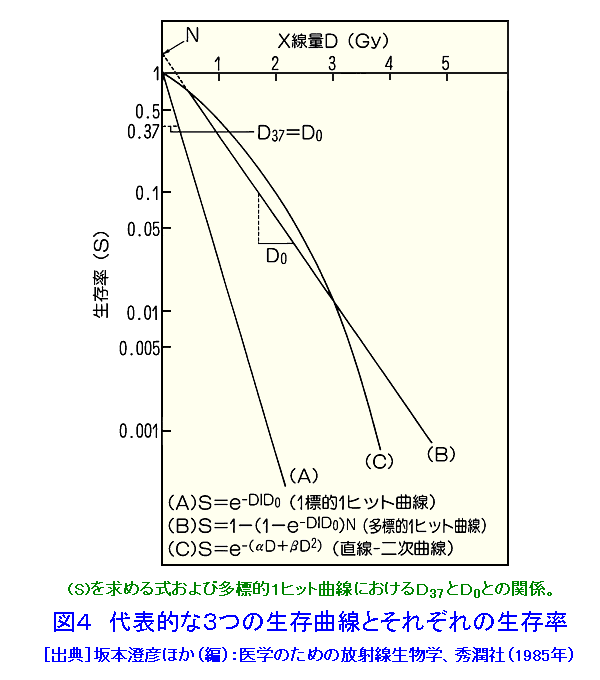
１　線量効果関係モデル
　放射線生物学や放射線医学等の分野では、線量と細胞の生物効果との関係（線量効果関係）を明らかにすることは重要である。生物効果の評価の方法は細胞死だけでなく、染色体異常、突然変異、細胞がん化に関連した細胞形質転換等いろいろあるが、放射線生物学では一般に細胞死を指標とすることが多いので、ここでは細胞死について述べる。線量と細胞死との関係をしめす線量効果曲線を線量−細胞生存曲線あるいは単に生存曲線という。ここでいう細胞死とは、実験的に、放射線を照射した細胞をシャーレの上で培養したとき、一個の細胞から増殖して可視的に計数できる一定以上の大きさの細胞集落（コロニー）を形成できる能力を消失することを指している。哺乳動物細胞の生存曲線は一般に図１（Ａ）に示すように縦軸、横軸を算術目盛りにとるとＳ字状の曲線を示し、縦軸を対数目盛りにすると、肩のある生存曲線を示す。また、バクテリアや特殊な哺乳動物細胞では図２に示すように指数関数曲線となるものがある。細胞死の分子機構は複雑で不明な点も多いので、照射（吸収）線量と生存曲線の関係を分子レベルで説明することはむずかしい。しかし、細胞の生存曲線の理論的説明の一つとして、「標的論」がある。これは微生物や代表的な哺乳動物細胞において実際に得られた生存曲線と適合するのでその説明に使われるが、標的論が正しいという証明ではない。さらに、哺乳動物細胞の標的は２重鎖構造をもつ遺伝子DNAであるとみなして、直線−二次曲線モデル（LQモデル；Linear Quadratic Model）も作られている。
２　標的論
　標的論とは、細胞内には細胞としての機能を維持するために必要不可欠な場所（標的）があって、この標的が放射線でヒットされ障害されると、細胞死がおこるという考え方である。この場合、ヒットには中間の型は存在せず、すべて（all）か、なし（non）であり、しかも互いに独立におこるとするものである。標的数とヒット数の組合せにより以下の４つのモデルが考えられている。この考え方は、必ずしも放射線の細胞内の標的が遺伝子DNAであるという前提で成り立っているものではないが、現在では分子生物学の進歩によって、哺乳動物における放射線の標的となりうる条件をみたす分子はDNAであることが明かになっている。
　ｉ）１標的１ヒット型
　１つの細胞内に存在する標的は１個だけであり、ここに1個のヒットが生じると細胞死が起こる。この型の生存率を示す致死効果をグラフに示すと図２の様に指数関数型を示すことになる。例として、バクテリアと特殊な哺乳動物細胞がある。
　ii）多標的1ヒット型
　１細胞当り（Ｎ個）の標的があり、その各々に少なくとも１個以上のヒットが生じるとはじめて細胞死が起こる。この型の生存率を示す致死効果をグラフに示すと図１の様な肩のある曲線になる。例として、一般的な哺乳動物細胞がある。ここでの標的数は図３及び図４の外挿値（Ｎ）である。
　iii）１標的多ヒット型
　１つの細胞内にある標的は1個であるが、この標的に複数（Ｍ個）のヒットが起きたときに細胞死が起こる。取扱いが複雑であまり使われない。
　iv）多標的多ヒット型
　１細胞内にＮ個の標的があり、各標的にＭ個のヒットが起こったときに細胞死が起こる場合である。取扱いが複雑であまり使われない。
　１標的１ヒットの標的論から導かれた重要な考え方に平均致死線量がある。これは、すべての標的に平均１個ずつのヒットが生じるのに相当する線量をいう。集団中の細胞の全ての標的に平均１個ずつのヒットが生ずるということは、いいかえると、ヒットの起こり方は、ランダムであるために、集団の個々の細胞においては、同じ標的に２個も３個もヒットされるものもあり、また、まったくヒットが起こらないものもある。確率論的にいって、平均１個ずつのヒットが生じるときに、まったくヒットが起こらない細胞、すなわち、死なないで生存する細胞数は37％の場合に相当する。したがって、平均致死線量は、37％の生存率をもたらす線量でもあるところから、37％生存率線量ともいい、Ｄ37と表すことがある。図４の（Ａ）線におけるＤ37は、縦軸で0.37を示す点における横軸の座標の線量Ｄである。
　また、多標的１ヒットの標的論から導かれたものにＤ0と外捜値（Ｎ値）があり、これらは細胞の放射線感受性を左右する生存曲線の重要なパラメータである。縦軸を指数関数目盛りにして生存率を、横軸を普通目盛りにして線量をとると生存曲線は、指数関数型では直線にＳ字型では低線量域では上に凸の曲線を示し（肩がある）、次第に直線に移行する。図３にこれを示す。後者のような場合には、生存曲線の直線部分で、生存率を37％まで減らすのに必要な線量をＤ0という。Ｄ37と異なって、Ｄ0は平均致死線量ではないので区別すべきであるが、実際には明確な区別をしないで同じような意味で使われていることが多い。厳密には図４の（Ｂ）線上の直線部分において生残率が37％減少するのに要する線量を表す。図３または図４の（Ｂ）線上の直線部分を破線で延長し縦軸と交わったところを外捜値（Ｎ値）といい、これは多標的１ヒット論における細胞内の標的の数を表すものである。例えば図３においてＮ値が５とある場合には４ヶ所のヒットまでは、その細胞は生存し致死的損傷を被っていないことを意味する。哺乳動物の生存パラメータであるＮ値およびＤ0は生物種によって、同一個体でも組織によって、あるいは正常細胞と腫瘍細胞によって（また同じ細胞でも細胞周期によって）も異なっている。哺乳動物細胞においては通常、Ｎ＝1〜10、Ｄ0＝1〜2Gyの範囲にある。
　最近の研究で、二重鎖切断の修復を取り入れたモデルも検討されている。
３　直線−二次曲線不活化モデル
　放射線の細胞死に係わる標的は遺伝物質のDNAであるという放射線生物学的知見や、標的をDNAに絞り、しかも、これの二重鎖構造を重視して、有効致死損傷は、１本鎖切断よりも修復困難な２本鎖切断であるという考え方に基づいたモデルとして、直線−二次曲線不活化モデルが作られた。このモデルはDNA損傷の修復という要素も導入しているため、その分子機構は複雑である。上に述べた標的論のヒットがall-or-noneであって中間型が存在しない考え方に立っているのと異なって、直線−二次曲線不活化モデルでは、DNA修復が生じるため単独では有効致死損傷とはならない１本鎖損傷という中間型ヒットと有効致死損傷となりうる２本鎖切断による有効致死損傷つまり完全なヒットとが存在するという考え方に立っている。要するに、最終的な有効致死損傷の発生率を確率的現象として捕らえたものである。これを数式で表してみると次のようになる。１粒子による２本鎖切断の発生率をαとし、２粒子による１本鎖切断が近距離にあって２本鎖切断を起こす率をβの平方根とすると、αは線量Ｄに比例し、βは線量の２乗（Ｄ²）に比例するので致死率はαＤ＋βＤ²となる。したがって、生存率をＳとすると、
　　　　Ｓ＝exp［−（αＤ＋βＤ²）］
となる。このモデルはＸ線照射したチャイニーズハムスター細胞の生存曲線によく適合していることが示されており、図４のＣがこのモデルの示す曲線である。ちなみに、突然変異発生率と線量との関係はこの直線−二次曲線モデルが理論的に適していると考えられている。

＜図／表＞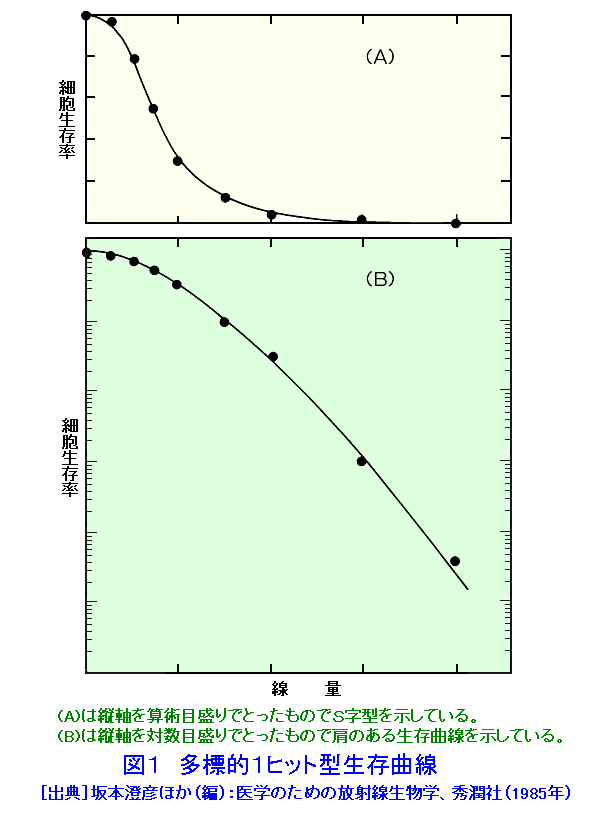

＜参考文献＞
（1）菅原　努ほか（編）：放射線細胞生物学、朝倉書院（1968年）
（2）近藤宗平：分子放射線生物学、東京大学出版会（1972年）
（3）坂本澄彦ほか（編）：医学のための放射線生物学、秀潤社（1985年）
（4）内海博司：古典放射線生物学を分子レベルで何処まで語れるか？、電離放射線の生物影響とDNA２重鎖切断の修復機構、日本放射線影響学会大会講演要旨集、43：51（2000年）