|
<解説記事ダウンロード>
<概要>
放射線と物質(媒質と同義に扱う)との相互作用には、放射線の種類とエネルギーが関係する。物質の種類も関係するが、相互作用を考えるさいは、むしろ原子の構成要素(原子核と束縛電子)のような微視的側面からの理解が必要である。最も基礎的な作用過程である原子の束縛電子との相互作用では、放射線の散乱や吸収が主な過程である。その過程で物質内には原子・分子の電離、励起、光放出などの作用が起きる。原子核との相互作用においては主に原子核反応を取り上げる。ただし、放射線と物質との相互作用の種類は極めて多く、しかも、そのエネルギー依存性が大きいため、2,3の項目の概要説明に止める。 <更新年月> 2004年02月 (本データは原則として更新対象外とします。)
<本文>
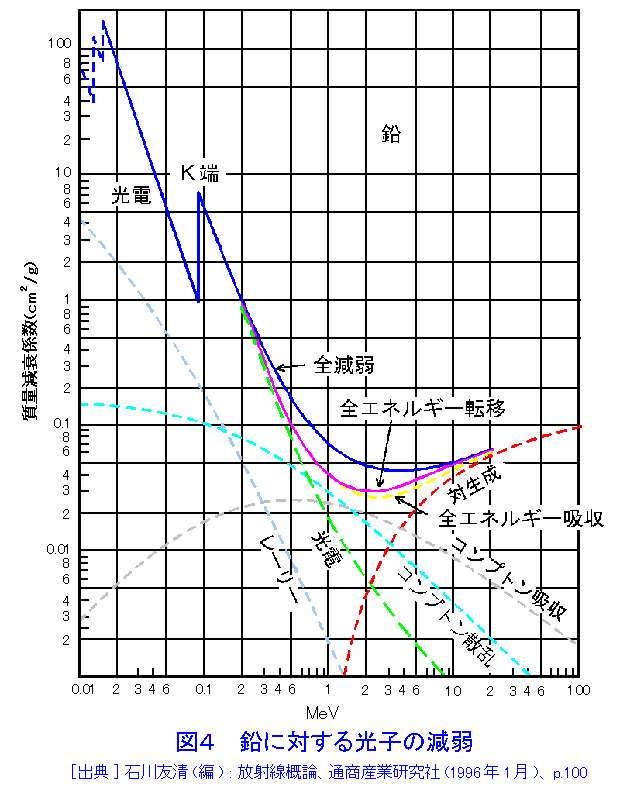
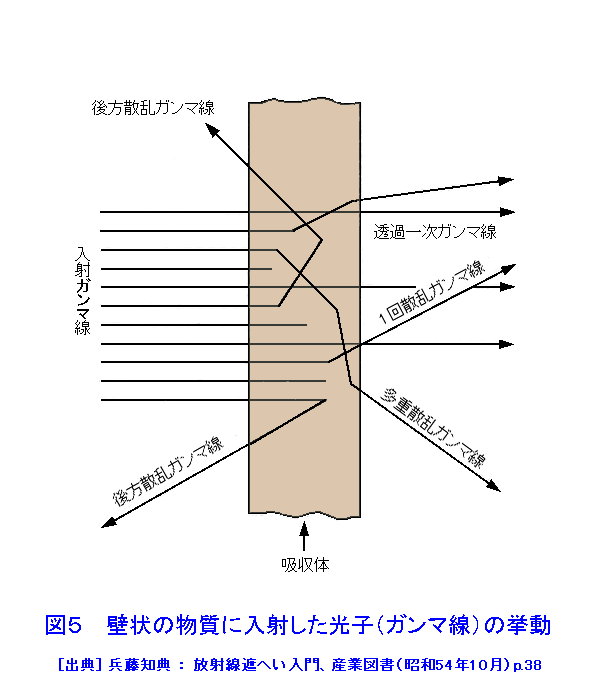
1.まえがき 放射線(電離放射線)と物質(ここでは媒質と同義に扱う)との相互作用の基は、外部から飛来する放射線というミクロな粒子(入射粒子)が、物質を構成しているミクロな粒子(標的粒子)と互いに作用を及ぼしあうことにある。つまり入射粒子が標的粒子と衝突して起こる現象の説明である。粒子どうしの衝突のさい、入射粒子が標的粒子に及ぼす力は、原子や分子の結合力に比べて圧倒的に大きい。原子核と電子の結合力は原子や分子の結合力よりも格段に大きいため、放射線と物質の相互作用を取り扱うさいに、これが中心的な課題になる。核子間に働く核力はさらに一段と大きいため、高エネルギーの放射線を扱うさいに問題になる。結合エネルギーとは反対に、作用が及ぶ空間的な距離は、原子と分子、原子核と電子、原子核内部の核子と核子の順に極端に小さくなる。 放射線には粒子線と電磁波(光子)があり、粒子線には荷電を有する荷電粒子線と荷電のない非荷電粒子線がある。放射線のエネルギーはさまざまである。そこで、まず放射性同位元素から放出される程度のエネルギーを有する放射線(10MeV以下)に的を絞って考えることにする。 2.放射性同位元素の崩壊により放出される程度のエネルギー(keV〜10MeV)の放射線と物質との相互作用 原子・分子系の外殻電子の結合エネルギーは数eVの程度であるのに対し、入射粒子が数MeVのエネルギーを有する荷電粒子の場合は、放射線のエネルギーが百万倍も大きい。そこで、物質中の電子に一万回以上も衝突を繰り返して、徐々にエネルギーを失う。荷電粒子と物質の相互作用の概念図を図1に示す。これにたいし電荷を持たない中性子や光子は、1回の衝突によって大きなエネルギーを失って、その結果荷電粒子を発生させる。そのため、荷電粒子では単位長さ当たりのエネルギー損失が問題になり、非荷電粒子では衝突断面積が問題になる。 2.1 荷電粒子のエネルギー損失 荷電を有する入射粒子のエネルギー損失過程には、弾性散乱、非弾性散乱、原子核反応と制動放射がある。粒子どうしの衝突において、入射粒子と同じ粒子が再び放出される場合と、入射粒子が標的粒子に吸収される場合がある。単独の粒子どうしの機械的な衝突が弾性散乱である。どちらかの粒子に内部構造がある場合は、衝突によって内部システムに変化が生じ、運動エネルギーの一部が移行する。これが非弾性散乱である。電子の場合に限り、原子核の近くで加速度を受けて放射される制動放射が有意に起こる。標的粒子の原子核に、エネルギーが吸収されて起こる過程が原子核反応である。入射粒子の一部は物質を通り抜ける。これを放射線の透過という。 物質の単位長さ当たりのエネルギー損失を阻止能という。入射粒子のエネルギー損失には衝突によるものと放射によるものとがある。単位長さあたりの減弱率(線減弱係数という)を質量で除した値を質量吸収係数[cm2/g]という。単位長さあたりの電離数を比電離と言う。図2は212Poから放出されるアルファ線のブラッグ曲線(比電離を示す)である。 放射性同位元素(RI)の崩壊により放出される放射線のエネルギーは、keV程度から10MeV程度までである。keV以下の放射線のエネルギー損失は、主に弾性散乱が支配的である。keV以上になると非弾性散乱が支配的になる。特殊な例を除き、原子核反応によるエネルギー損失の割合は小さい。 散乱された粒子が依然として高いエネルギー状態にあると、引き続いて散乱を繰り返し、数百eV以下に減速されると、二次的に発生した電子による電離作用や励起作用が支配的になる。気体における原子・分子の平均電離エネルギーの大きさは30eV程度、半導体の電離エネルギーは数eV程度である。減速過程には常に物質に特有の輻射を伴うが、ついには熱エネルギーが系全体に伝達される。 電子は荷電粒子であるが、標的粒子と衝突したときのエネルギー損失が大きく、ひとたび原子の束縛電子に衝突すれば、入射電子との区別がなくなる点で、その他の荷電粒子(荷電重粒子という)とは異なっている。べータ線は電子線であるが、そのエネルギーは0から最大エネルギーまでの連続スペクトルである。ベータ線の物質中での吸収曲線の例を図3に示す。電子の速度は同じエネルギーの荷電粒子のなかで著しく大きい。入射粒子が原子核の近くで加速を受けて放射される過程を制動放射というが、制動放射の放射率は標的粒子の質量の2乗に反比例する。電子の質量を電荷の等しい陽子の質量と比べると放射率は陽子の340万倍である。電子の場合に制動放射によるエネルギー損失が電離作用のそれと等しくなるのは、鉛で〜20MeV程度、水で〜200MeV程度である。 2.2 非荷電粒子のエネルギー損失 電磁波の量子である光子は、物質中では主にそれを構成する荷電粒子と相互作用する。主要なものに光電効果、コンプトン散乱、電子対生成の三者がある。図4に鉛における光子の阻止能とエネルギーの関係を両対数値で示す。光電効果の寄与とコンプトン散乱の寄与が等価になるのはおよそ0.7MeV、コンプトン散乱と電子対生成の場合はおよそ4MeVである。物質中で電子と陽電子対を生成するには光子のエネルギーは少なくとも1.02MeVを上回る必要がある。巨視的に見た光子の散乱、吸収の様子を図5に示す。コリメートした光子の入射方向の光子数を計測すると、指数法則に従う減弱の測定ができるが、一般に、厚い物質を通過する広い線束を測定するさいには、幾何学的条件で定まるビルドアップを補正しなくてはならない。ただし、ビルドアップ係数は特定の配置ごとに求める必要がある。光子は後方散乱する。半空間全体の後方散乱線束を光子数アルベドまたはエネルギーアルベドという。散乱体の厚さが増すとアルベドは飽和する。 中性子と物質の相互作用では束縛電子との相互作用は小さい。このさいは原子核との相互作用が主になる。弾性散乱、非弾性散乱、捕獲及び原子核反応がその例である。中性子のエネルギーが1MeV以下では、弾性散乱が優勢である。散乱中性子の方向分布を球対象として求めた衝突後の中性子エネルギーは、一回衝突ごとに初期エネルギーの1/eξになる。この関係を用いると初め1MeVであった中性子が熱中性子になるまでに必要な衝回数は軽水素で17.5回になる。1MeV〜数MeVの中性子は弾性散乱と非弾性散乱で減速する。さらに中性子のエネルギーが大きくなると中性子を吸収して陽子、アルファ線のような荷電粒子を1個放出する原子核反応が起こる。原子核反応では粒子の放出に伴って光子の放出が起こることが多い。熱中性子の捕獲反応断面積は原子核の種類によって著しく大きいものがある。113Cdや157Gdなどはその例である。熱中性子を吸収して光子を放出する(n,γ)反応も起こる。 非荷電粒子の散乱や反応で生じた荷電粒子の物質との相互作用は、放射線の種類とエネルギーに応じて、1.で記したものと同様の過程で減速し、類似の過程でエネルギーが物質に移行する。原子核反応によりエネルギーの出入が起こる。そのため、個々の反応のエネルギー収支を求めなければならないが、RIの崩壊で発生するエネルギー範囲では、特別な例を除きエネルギー損失に占める原子核反応の寄与は大きくない。 3.高エネルギーの放射線と物質との相互作用 高エネルギーの領域では入射粒子の速度が速くなる。荷電粒子の電離によるイオン対の生成率は速度に反比例(表1参照)する。それに反して原子核反応は種類が増加し、一回の衝突で原子核から放出される荷電粒子の種類や数も増加する。また、重い原子核以外の核分裂反応、核破砕反応、中間子の放出なども起こる。その結果、放射線と物質の相互作用に占める電離作用の割合は、高エネルギーの領域では減少し、原子核反応の割合が増加する。エネルギーが2GeVの陽子が、厚さ2.45cmの鉛で吸収されるエネルギー損失の例では、電離作用の割合が3%以下であるのに対し、原子核反応の割合は15%であったという。非荷電粒子線の場合も事態は同様である。 同じエネルギーの荷電粒子線のなかで、電子の速度は最も大きい。3MeVの電子の速度は、真空中での光速の99%に達するが、陽子では5.7GeVの速度に相当する。 表2に電子の速度と比電離能を示す。相対論的に有意な考慮が必要な領域では、制動放射損失が速度とともに大きくなる。 <図/表> 
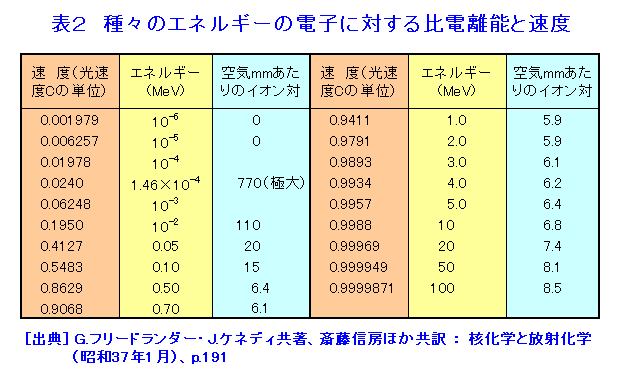
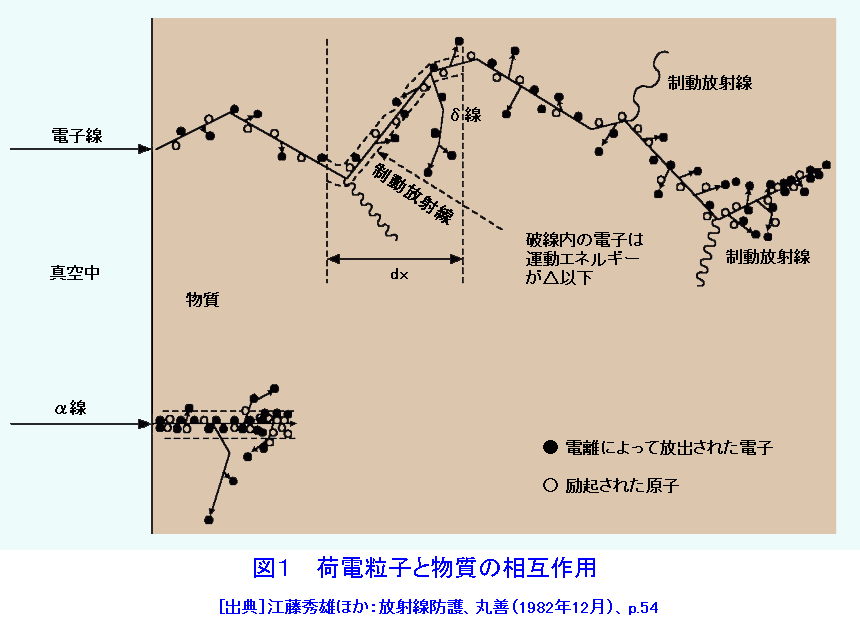
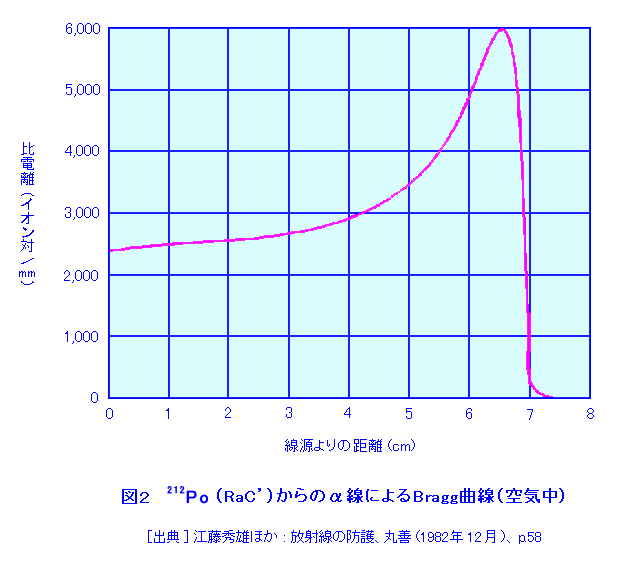
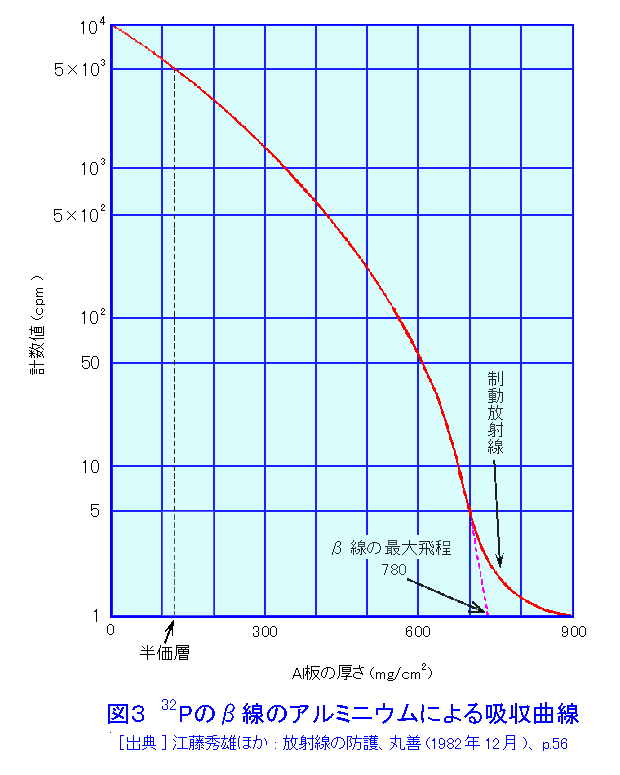
<関連タイトル> 放射線の分類とその成因 (08-01-01-02) 放射線の吸収エネルギー (08-01-02-01) 放射線の電離作用 (08-01-02-02) 放射線の遮へい (08-01-02-06) <参考文献> (1)成田正邦、小澤保知:原子工学の基礎、現代工学社(1989年1月) (2)野中到:核物理学、培風館(昭和31年8月) (3)物理学辞典編集委員会(編):物理学辞典(改訂版)、培風館(1992年5月) (4)石川友清(編):放射線概論、通商産業研究社(平成3年4月)
|

