＜本文＞
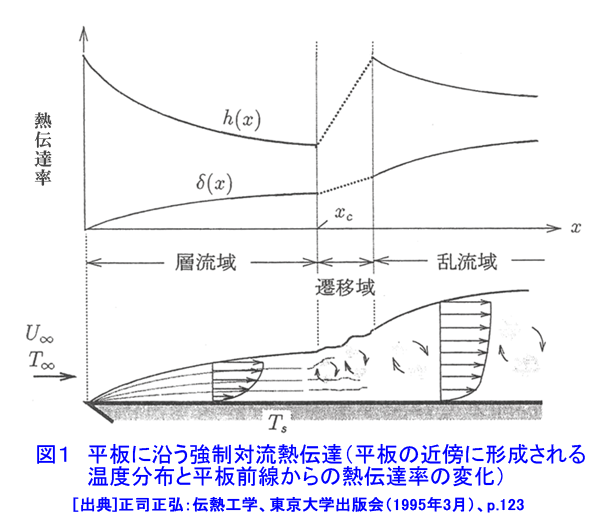
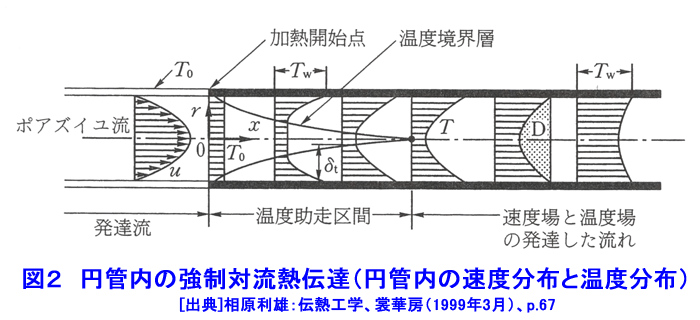
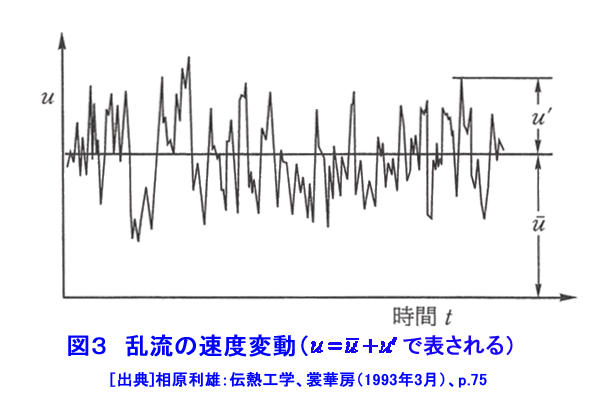
１．対流伝熱
　燃料棒や熱交換器など原子炉を構成する構造物は全て構造物の周囲を取り巻く流体の流れと熱の授受を行う状況下に置かれており、構造物は周囲を流れる流体によって冷却されたり、加熱されたりしている。このような構造物と流体との間の伝熱が対流伝熱である。もちろん、流体中の伝熱を扱うのも対流伝熱であるが、構造物の設計上重要となるのは構造物と冷却材等流体の流れとの間の伝熱である。対流伝熱は流体中の温度勾配に沿って流れる熱移動（熱伝導と呼ぶ）と流体自身の運動に伴うエンタルピ輸送の両者によって行われる。構造物の周囲を流れる流体の流れは、ポンプやブロアーなどによって強制的に作られる流れと構造物によって加熱されたり冷却されたりすることによって誘起される流れとがある。強制的な流れと構造物との間の伝熱を強制対流伝熱と呼び、加熱・冷却によって誘起される流れと構造物との間の伝熱を自然対流伝熱と呼ぶ。冷却材の流れによる燃料棒の冷却や熱交換器内における冷却材の流れと熱交換器伝熱管との間の伝熱等は強制対流伝熱であり、原子炉停止時における燃料棒と冷却材との伝熱、原子炉容器と容器外側の空気・容器内側の冷却材との伝熱は自然対流伝熱である。
1.1　熱伝達率
　構造物の表面から流体に伝わる伝熱量は次式で求められる。
　　表１式（1）参照　　（以下、「式（2）から式（13）」は表１参照）
　qＷ［W/ｍ²］は構造物表面における熱流束であり、単位面積・単位時間に構造物表面から流体に伝えられる熱量（TW＞Tfの場合）、または、流体から構造物表面に伝えられる熱量（TW＜Tfの場合）を表す。TWとTfは構造物表面の温度と流体の代表温度を表す。h［W/（ｍ²・K）］を熱伝達率と呼ぶ。熱伝達率は流体の種類と状態（温度や圧力）のみによって定まる値ではなく、流体の種類・状態の他に、構造物表面の粗さ・形状（フィン、突起面、平滑面等）、流速、流路形状（円管、二重管、三角流路等）及び流れの状態（層流、乱流、遷移流）などによって異なった値となる。構造物の表面では流体は止まっており、流体の流速はゼロであるので構造物の表面においては流体運動によるエンタルピ輸送は行われない。すなわち、例え対流伝熱であっても、物体表面に接する流体中では熱伝導のみによって熱移動が行われる。したがって、熱伝導に対するフーリエの法則（式（2））が成立する（詳しくは原子炉の熱流動IIを参照）。式（1）と式（2）より式（3）が得られる。
　λ［W/（m・K）］は流体の熱伝導率であり、nは構造物の表面に垂直にとった座標である。この式から分かるように、熱伝達率は構造物表面に接する静止流体中の温度勾配に比例した値である。
1.2　強制対流熱伝達の基礎式
　構造物表面における流体の温度勾配が求まれば、式（2）を用いて構造物から流体への伝熱量（＝構造物表面における熱流束qW）を求めることができるし、式（3）を用いて熱伝達率を求めることができる。また、流体の温度分布と速度分布が分かれば流体中におけるエネルギーの輸送状況（エンタルピ輸送と熱伝導）を求めることができる。流体の温度分布はエネルギー保存の式（式（4））を適切な境界条件と初期条件の下で解くことにより求めることができる。
　上式（式（4））を解くためには流速分布（u，v，w）が必要である。流速分布は、連続の式（式（5））と運動量保存の式（式（6）〜（8））を適切な境界条件と初期条件の下で解くことにより求めることができる。
　図１に平板に沿って流れる強制対流によって平板の近傍に形成される温度分布と平板前縁からの熱伝達率の変化を示す。δは温度が変化する範囲（温度境界層の厚み）を示す。図２には円管内を流れる層流強制対流の速度分布と温度分布を示す。原子炉では、流れが乱流である場合が多い。乱流の流速や圧力及び温度は常に変化しているため、式（4）〜式（8）のような非定常方程式（時間変化の項を含んだ方程式）を解く必要があるが、これらの方程式を解析的に解くことは難しい。また、数値解析によって解くことのできる場合も限られている。しかし、原子炉構造物を含め一般の工業機器は大きな熱容量を持っているため、乱流の変動周波数に比べて構造物の応答周波数は極めて低い、したがって、原子炉構造物の設計に当っては、時々刻々変化する乱流の速度変動や温度変動そのものを知る必要がなく、ある程度の時間間隔で平均した流速や温度の時間平均値が分かれば十分である。このような場合には、速度、圧力、温度を次式のように、時間平均値と時々刻々変化する変動値の和で表すことができる（図３参照）。
　式（9）を式（4）〜（8）に代入してそれぞれの式に時間平均操作を施すと同時に、乱流モデルを組み込むことによって、速度、圧力、温度の時間平均値を求める基礎式（連続の式、運動量保存の式、エネルギー保存の式）を得ることができる。このようにして得られた新しい基礎式を数値解析することによって速度分布、温度分布、熱流束分布等を求める場合が多いが、現在では未だ数値解析結果と実験結果の両者を使って熱設計や、異常時、事故時の熱解析が行われている。原子炉の定常運転時のように、流れが時間的に変化しない定常流の場合には、左辺第1項を除いた運動量保存の式とエネルギー保存の式を解くことによって、速度分布や温度分布が求まる。
　また、事故時や異常時の熱解析では、自然対流を取り扱う必要がある。自然対流の流速分布を求めるには、浮力による流れの駆動力を表す項を追加した運動量保存式が用いられる。図４に加熱物体の周りに形成される自然対流の例を示す。
1.3　対流熱伝達率の整理式
　計算機の発達によって連続の式、運動量保存式、エネルギー保存式を数値解析によって解き、強制対流や自然対流の熱伝達率を理論的に求める試みが多く行われるようになりつつあるが、原子炉の設計に当っては実験式を必要とされる場合が極めて多い。また、理論的に求めた熱伝達率を適切な整理式にまとめておくと設計者等にとって極めて便利である。熱伝達率の値は流体の種類、流速、流路寸法が異なると異なった値となるので、熱伝達率の値そのものを整理式の形にまとめようとすると膨大な数の整理式が必要となる。しかし、熱伝達率を適切な無次元数の間の関係式でまとめると、流路形状が同じであれば、流体の種類、流速、流路寸法には無関係な一つの整理式にまとめることができる。熱伝達率は次のような無次元量の間の関係式でまとめられることが多い。
　 強制対流熱伝達率の整理式　：　式 （10）
　 自然対流熱伝達率の整理式　：　式 （11）
　Nuはヌッセルト数、Reはレイノルズ数、Prはプラントル数、Grはグラスホフ数であり、いずれも対流熱伝達率の整理式を作成する際の重要な無次元数である。（定数）、n及びmは流路の形状及び流れの状態（層流か乱流）等によって異なった値となる。U，Lはそれぞれ流速と流路寸法を表す代表値である。例えば、円管内の流れであれば、Uは平均流速を用い、Deは円管の直径を用いる。原子炉の設計や安全解析に当っては文献等に記載されている熱伝達率の整理式を使用することが多いが、流速や流路寸法の代表値であるU，Deとしてどんな値が用いられているかについて十分に注意する必要がある。λ，ν，μ，Cp，β，Δθはそれぞれ、流体の熱伝導率、動粘性係数、粘性係数、定圧比熱、対膨張係数、構造物の表面温度と流体温度との差である。
　例えば、円管内の流体と円管壁との間の強制対流熱伝達率は式（12）で表される。
　また、円管外の自然対流熱伝達率は式（13）で表される。
　炉心内の燃料棒群、熱交換器の伝熱管群と冷却材との間の熱伝達率等、多くの形状の流路に対して熱伝達率の実験式が求められている。
　熱伝達率の整理式が求められていない場合には、新たに実験等を行って熱伝達率等を求める必要があるが、熱伝達率は上式のような無次量の間の関係で整理できるので、必ずしも実機と同一寸法、同一作動条件下で実験を行う必要が無い。レイノルズ数、プラントル数、グラスホフ数が同じ値になるような条件であれば、実験の容易な縮尺モデル、作動流体、流速範囲を選んで実験を行えば良い。
　表２と図５に強制対流熱伝達率の実験式の例を示し、図６に自然対流熱伝達率の例を示す。

---

＜図／表＞

---

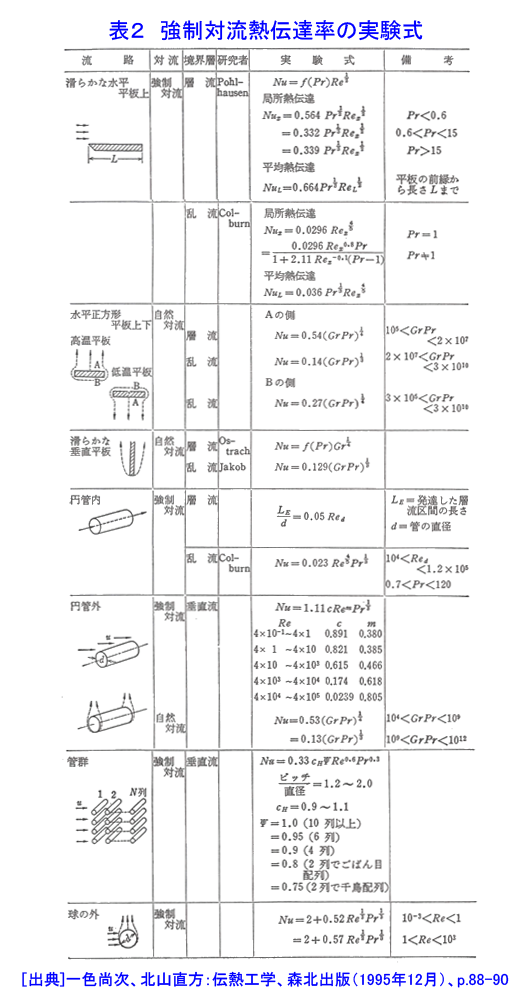
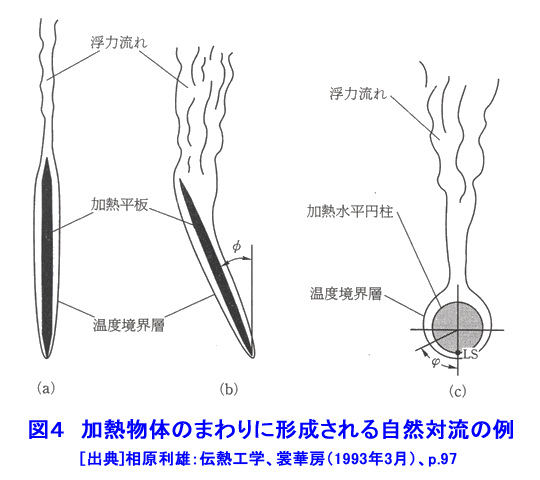
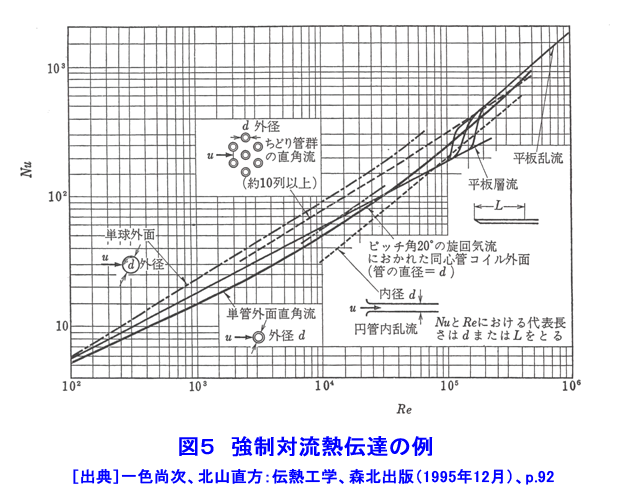
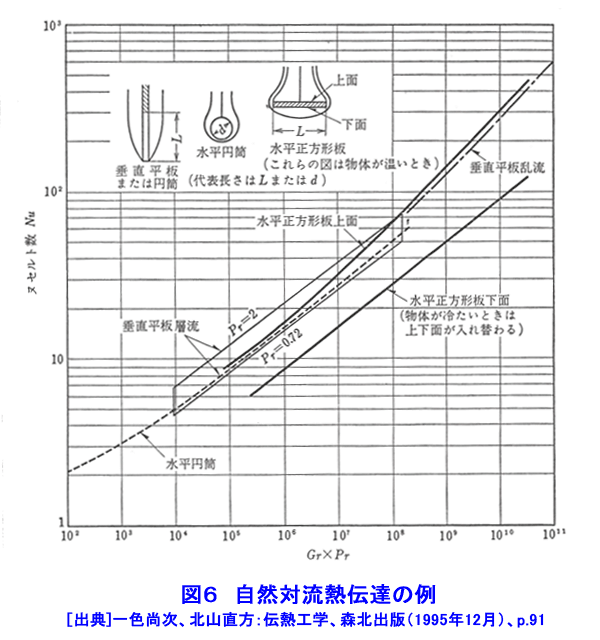
＜関連タイトル＞
原子炉の伝熱流動（2） (03-06-02-02)

---

＜参考文献＞
（1）一色尚次、北方直方：伝熱工学、森山出版（1995年12月）、p.88-92
（2）正司正弘：伝熱工学、東京大学出版会（1995年3月）、p.123
（3）相原利雄：伝熱工学、裳華房（1999年3月）、p.67-97

---