原子炉の伝熱流動（2） (03-06-02-02)

＜本文＞
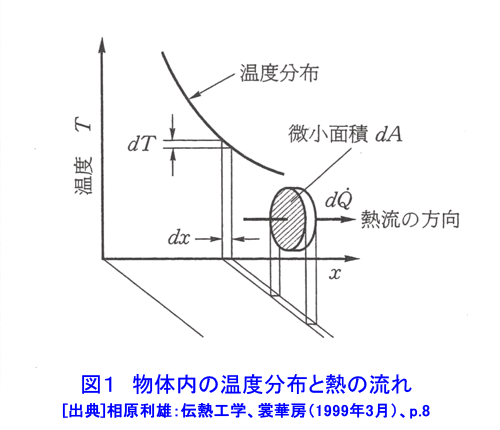
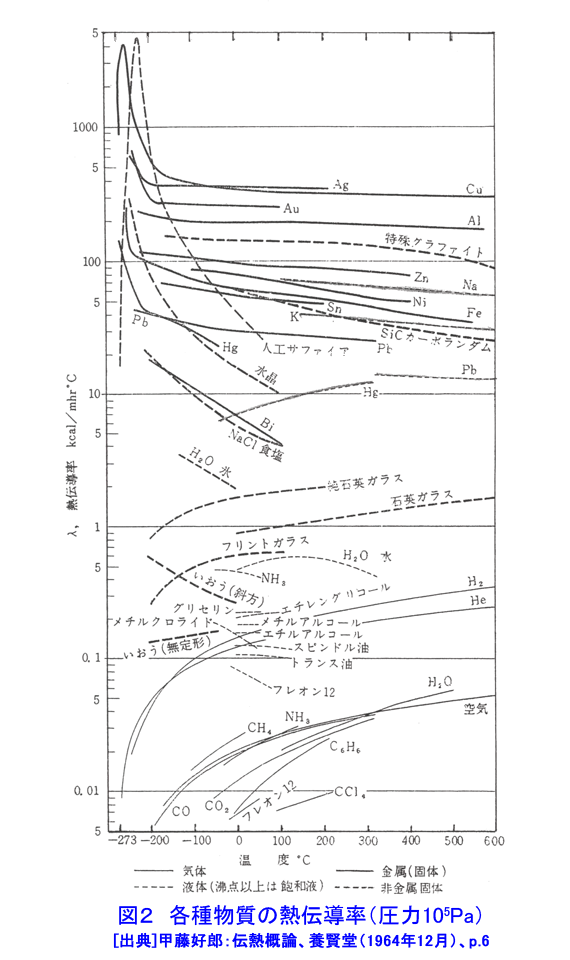
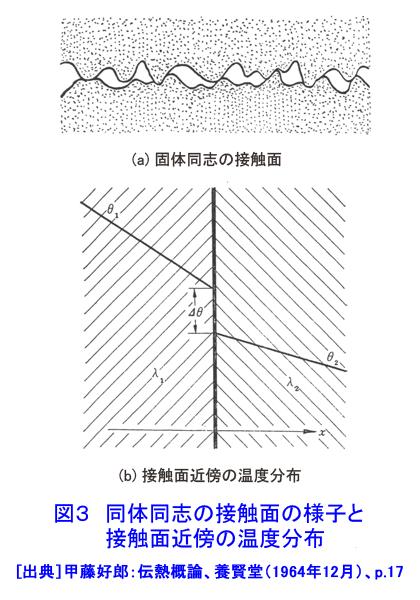
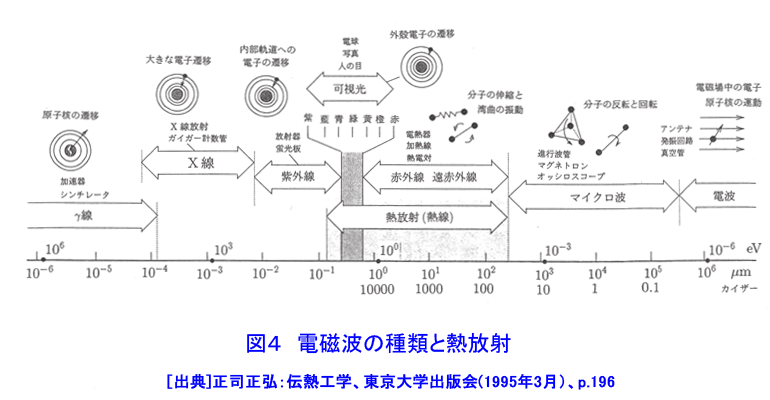
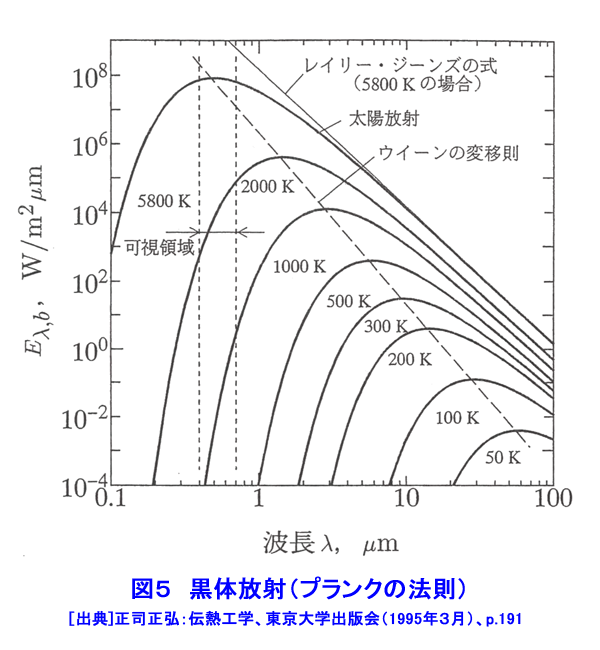
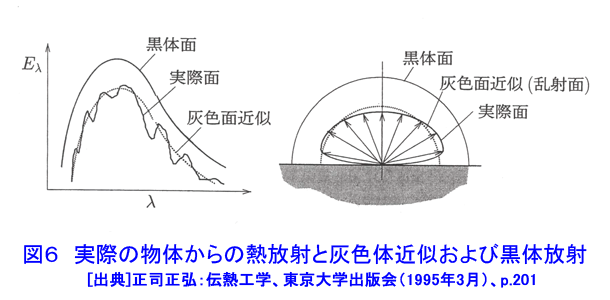
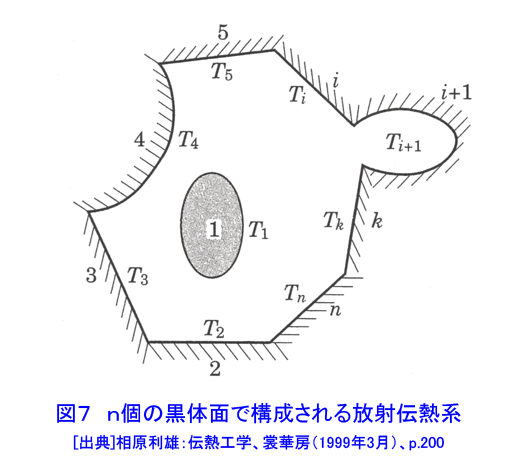
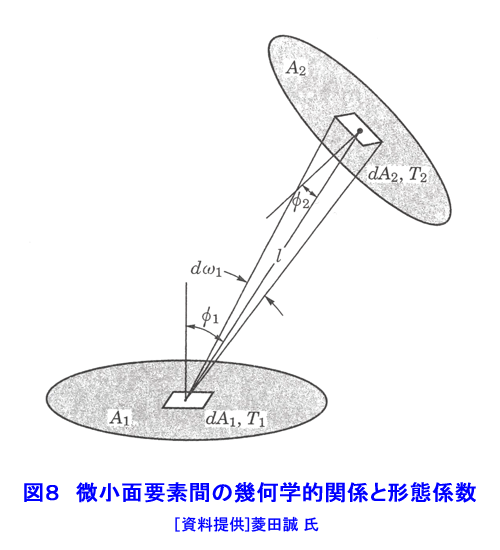
１．熱伝導
　熱伝導は、物体中の温度分布に沿って、温度の高いところから温度の低いところに向かって熱が流れる現象である。気体や液体中では、分子あるいは原子の熱運動によって熱が高温部から低温部へ伝えられる。熱伝導により伝えられる熱は、フーリエの法則（次式）によって与えられる（図１参照）。
　　　　　表１　式（1）参照　　　（以下、「式（2）から式（15）」は表１参照）
　q［W/ｍ²］は熱流束であり、単位時間内に座標xに直角な単位面積を通過する熱である。Ｔ［K］は温度である。λ［W/（m・K）］は熱伝導率と呼ばれ、その値は物質の種類とその状態（温度と圧力）によって定まる。熱伝導率は物質内に同じ温度分布が生じる場合の熱の伝わり易さを表す尺度である。金属では自由電子の熱運動、非金属では結晶格子の熱弾性運動、液体では分子の振動運動、気体では原子・分子の熱運動により熱伝導が行われる。このように、物質によって熱伝導の機構が異なるため、熱伝導率も物質によって大きく異なる。大まかに言って物質の熱伝導率は最も大きいので5000W/（m・K）程度であり、最も小さいもので0.005W/（m・K）程度である。熱伝導率が最も大きいのは金属であり、以下、非金属、液体、気体の順になっている（図２参照）。断熱材は非金属繊維の物が多いが、断熱材の熱伝導率が小さいのは、断熱材の素材そのもの熱伝導率が小さいのではなく、断熱材中の微小空間に閉じ込められている空気の熱伝導率が低いことと、繊維が曲がりくねっているため熱の伝わる距離が長くなること、繊維同士の接触が点接触に近い形で行われるため、繊維間の熱移動が極めて困難になるためである。通常の状態では繊維断熱材中に含まれる微小空間の合計は全体体積の約95％に達する。
　原子炉の燃料要素と被覆管などのように固体同士が接している接触面で見かけ上温度ギャップが生じることがある。この温度ギャップが生じる原因を接触熱抵抗と呼ぶ。固体の表面には粗さがあるため物体間の接触面は完全に密着しているわけではなく、多くの空間がありその空間の中には通常気体が入っている。接触面を実際の接触状態に合わせて温度分布を求めることは極めて困難であるので、実用上は接触面を完全な平面接触として取り扱い、接触熱抵抗から求めた温度ギャップで補正を行う。接触面での温度ギャップは次式で求められる（図３参照）。
　　　　式（2）
　RH［ｍ²K/W］が接触熱抵抗であり文献などに記載されている実測値や整理式から求める。接触熱抵抗は燃料棒など熱流束が大きい場合に重要となる。
燃料棒、原子炉容器、熱交換器等の構造物を設計するためには、構造物内の温度分布や熱流束分布を求める必要がある。構造物の温度が時間的に変化する場合の温度分布は次式で表される非定常熱伝導の基礎式（3）を解くことによって求められる。
　　　　式（3）
熱伝導率λが一定値とみなせる場合は次式となる。
　　　　式（4）
　W［W/ｍ³］は崩壊熱やγ線加熱などによる構造物内部における単位体積当たりの発熱量である。また、ρとCは構造物の密度［kg/ｍ³］と比熱［J/kg・K］である。λ/（ρC）［ｍ²/s］は温度伝導率又は熱拡散率と呼ばれ、温度分布の時間的変化の速度を左右する重要な物性値である。上式を構造物の使用条件を適切に表した境界条件（例えば、構造物表面における温度や熱流束）と初期条件（初期状態における構造物の温度分布）の下で解くことにより温度分布の時間変化を求めることができる。また、原子炉の定常運転時における燃料棒、熱交換器等の温度は時間的に変化せず一定である。このような場合の温度分布（定常温度分布）は次式を適切な境界条件の下で解くことによって求めることができる。
　　　　式（5）
　計算機が発達する以前には、種々の形状をした物体中の温度分布の解析解を種々の境界条件、発熱量分布、初期条件の下で求める研究が盛んに行われ、その成果の集大成は、例えばH.S.Carslaw and J.C.JAEGERの本（1）等にまとめられている。しかし、実際の構造物のように複雑な形状をした物体内の温度分布を解析的手段によって求めるのは非常に困難である。計算機が発達した現在ではほとんどの場合数値解析によって温度分布が求められており、数値解析を行うための市販の計算プログラムも多数販売されている。解析解は数値解析方法の妥当性を検証するために使用されていると言っても過言ではなくなりつつある。
２．熱放射（放射伝熱）
　熱放射は物体がエネルギーを電磁波の形で放出したり吸収したりする現象である。物体を構成する分子や原子は複雑な熱運動をしているため、これに付随する電子の運動によって電磁波が放射される。分子や原子の熱運動の激しさは温度によって決まるため、物体の放出する熱放射の性質（波長やエネルギー）も物体の温度だけで定まる（図４参照）。熱放射は離れた物体同士の間で直接エネルギーの授受が行われる伝熱形式である。放射伝熱においてはその物体から放射される熱放射エネルギーの放射特性とその物体に入射する熱放射エネルギーの吸収特性である。物体からの熱放射エネルギーは、その物体の温度、波長、放射の方向によって異なる。物体に入射する熱放射エネルギーの吸収特性は物体の温度と入射する熱放射エネルギーの波長等によって異なる。
2.1 黒体の熱放射特性と吸収特性
　完全黒体（以下、黒体）は温度T［K］の物体が放射できる最大の熱放射エネルギーを放出する仮想的物体（理想化された物体）であり、実際の物体の熱放射特性を調べる上で基本となる物体である。黒体から放射される熱放射エネルギーはどの方向に対しても同じ値である。また、温度Tの黒体1［ｍ²］から1［s］の間に半球空間に向かって放出される熱放射エネルギーの中で波長λの電磁波のもつエネルギーを単色放射能と呼び次式で求められる。これをプランクの法則と呼ぶ。
　　　　式（6）
　上式の計算結果を図５に示す。図に示すように、黒体からの熱放射エネルギーはある波長で最大となる。熱放射エネルギーが最大となる波長λmax［μm］は黒体の温度T［K］によって異なる。 λmaxとTとの間には次の関係がある。この関係をウイーンの変移則と呼ぶ。
　　　　式（7）
　式（6）を全波長域に渡って積分すれば、温度Tの黒体1［ｍ²］から1［s］の間に半球空間に向かって放出される熱放射エネルギーの全量を求めることができる。これを全放射能Eｂと呼び次式で与えられる。これをステファン・ボルツマンの法則と呼ぶ。
　　　　式（8）
　周囲から物体に入射する熱放射エネルギーの吸収特性についても黒体が基本となる。黒体は射する熱放射エネルギーを全て吸収する。
2.2 灰色体の熱放射特性と熱放射吸収特性（実際の物体をモデル化した物体）：
　実際の物体からの熱放射エネルギーは黒体のようにどの方向にも一様な値ではなく放射の方向によって異なる。また、それぞれの波長の持つ熱放射エネルギーも物体と波長によって様々な値をとり、同じ温度の物体が放射する全放射能も物体の種類によってまちまちである。従って、現在では実際の物体からの熱放射をそのまま取り扱うことは極めて困難な状況である。そこで、実際の物体を灰色体でモデル化（灰色体近似）することによって放射伝熱を取り扱う（図６参照）。灰色体は黒体と同様にどの方向にも同じ強度の熱放射エネルギーを放出する物体であり、単色放射能Ｅλと全放射能Eは次式で求められる。
　　　　式（9）
　εは放射率であり、物質の種類と温度によって異なる値となるが波長によっては変わらない。灰色体に入射する熱放射エネルギーの内吸収するエネルギーは次式によって表される。
　　　　式（10）
　Hは物体に入射する全入射エネルギー、Hλはその内波長λの入射エネルギー、Qは物体が吸収する全エネルギー、Qλは物体が吸収する熱放射エネルギーの内波長λの持つ熱放射エネルギーである。αを吸収率と呼ぶ。キルヒホッフの法則によれば、灰色体の放射率と吸収率は等しい（ε＝α）。したがって、実際の物体をモデル化した灰色体の熱放射特性と熱放射吸収特性は放射率（＝吸収率）のみで表されることになる。
2.3 黒体間及び灰色体間の放射伝熱（黒体放射系及び灰色体放射系の伝熱）
　熱放射エネルギーを放射・吸収することによる物体間の放射伝熱は、物体を温度が一様であると近似できる幾つかの部分に区切り温度の異なる部分間の熱放射エネルギーを求める。例えば、図７に示されるような放射伝熱系において全ての部分を黒体で近似できる場合には、黒体面（i）から他の面に放射伝熱により伝えられる正味の伝熱量は次式で求められる。
　　　　　式（11）
　ここで、Aiは黒体面（i）の面積、Fikは面（i）と面（k）との間の形態係数と呼ばれ、2面の間の純幾何学的な関係から決定される。Fikは次式で定義される（図８参照）。
　　　　　式（12）
　次に、全ての面を黒体とみなすことができず、灰色体でモデル化する場合には、灰色体面（i）から他の面に放射伝熱により伝えられる正味の伝熱量は次式で求められる（図９参照）。
　　　　　式（13）
　ここで、Giは射度と呼ばれ灰色体面（i）の単位面積から単位時間の間に周囲に放射されているエネルギーであり、灰色体面自身から放射される熱放射エネルギー（式（14））に外来照射線の反射（式（15））を加え合わさった値である。上式に含まれる2n個の未知数GiとTiは2n個の連立一次方程式の解として求められる。

＜図／表＞

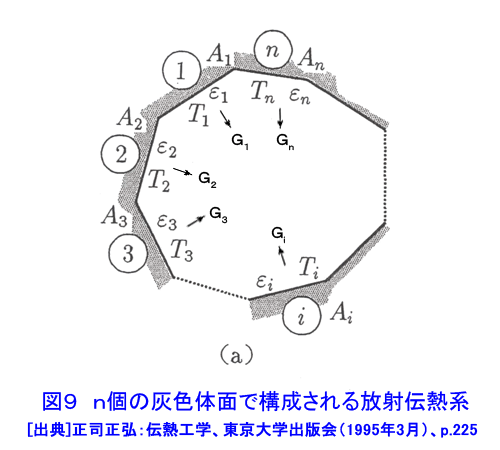
＜関連タイトル＞
原子炉の伝熱流動（1） (03-06-02-01)

＜参考文献＞
（1）H.S.Carslaw and J.C.JAEGER: CONDUCTION OF HEAT IN SOLIDS，OXFORD UNIVERSITY PRESS （1959）
（2）相原利雄：伝熱工学、裳華房（1993年3月）
（3）甲藤好郎：伝熱概論、養賢堂（1964年12月）
（4）正司正弘：伝熱工学、東京大学出版会（1995年3月）