β壊変 (08-01-01-06)

＜本文＞
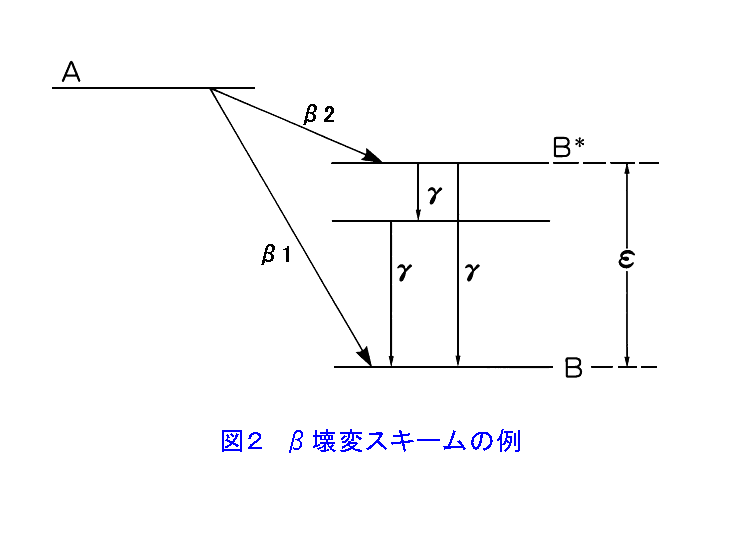
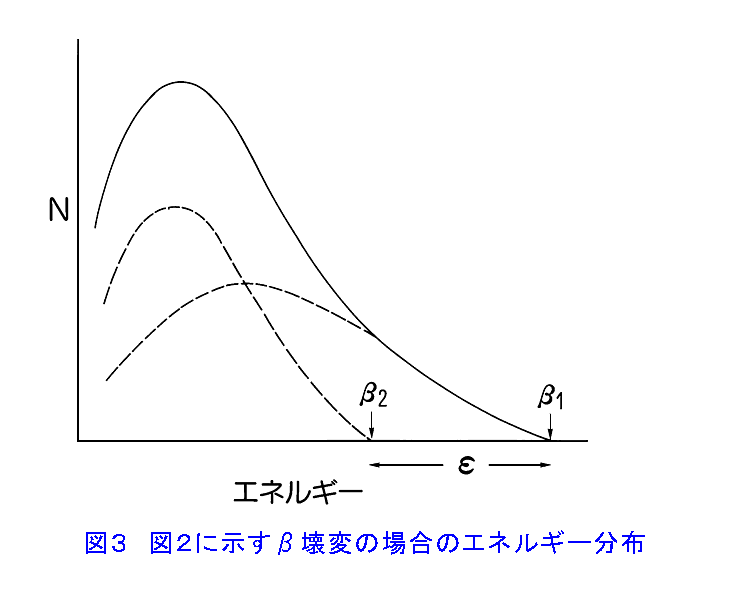
１．β壊変
　β壊変は、原子核または素粒子がβ⁻（電子）あるいはβ^＋（陽電子）を放出して、他種の原子核または素粒子に変化する現象である。たとえば、
　　　　中性子　　→　β⁻　＋　陽子
　　　　⁶⁴Cu　 →　β⁻　＋　⁶⁴Zn
　　　　²⁴Na　 →　β⁻　＋　²⁴Mg
　　　　¹¹Ｃ　　 →　β^＋　＋　¹¹Ｂ
などがそれである。
　また、陽電子を放出するかわりに原子核が軌道をまわる電子を吸収して陽子が中性子に変わる現象がある。湯川と坂田は、このような現象の起こる可能性を最初に予言した（1935年）。これを軌道電子捕獲といい、実験的にも証明されてβ壊変の一種であることがわかった。
　β壊変をする性質は、最初ラジウムやトリウム等の自然放射性核種で発見されたが、原子核反応による原子核の人工的な転換や原子核分裂の実験が進められるにつれて、多くの原子核がβ壊変をすることがわかった。
　β壊変では、核種の質量数は変わらない。β⁻壊変では原子番号が１だけ増加し、β^＋壊変や軌道電子捕獲では原子番号が１だけ減少する。

２．β壊変のエネルギー
　α壊変で放出されるα粒子のエネルギーは一定であるのに対して、β壊変で放出されるβ粒子（電子、陽電子）のエネルギーは、図１に示すようにそれぞれの核種に固有な上限値を持ったある分布（連続スペクトル）を持っている。このことに気付いたのはチャドウィック（Sir J.Chadwick，1914年）である。
　原子核は、それぞれに固有の離散的なエネルギー準位をもっている。したがって、β壊変で放出されるβ粒子のエネルギーが連続であることをどう解釈するかが1920年代後半の大きな問題であった。
　エリス（C.D. Ellis）とウースター（W.A. Wooster）は、RaE（²¹⁰Bi）を熱量計の中に入れ、β壊変で放出されるβ粒子を含む全ての放射線のエネルギーを測定した（1927年）。その結果、１個のRaE原子核の壊変によって、放出されるエネルギーは平均350±40keVという値を得た。この値は、RaEから放出されるβ粒子のエネルギースペクトルの最大値1050keVより小さく、むしろスペクトルの平均値390±40keVにほぼ等しい。このことは放出されるβ粒子が、核を離れる瞬間から観測されているような連続スペクトルを持っているということになる。その後、³²Ｐなどについても同様のことが確かめられた。そこでβ壊変の場合にはエネルギーの保存則は成立しないのではないかという意見が出てきた。
　1932年にチャドウィック（Sir J. Chadwick）が中性子を発見し、ハイゼンベルグ（W. Heisenberg）が原子核は陽子と中性子から成り立っているという理論を発表した。ここでβ壊変は次のような原子核内部での核内核子の変換と考えられた。
　　　　中性子 → 陽子＋ｅ⁻
この反応では、３個の粒子は共にフェルミ粒子なので、左辺の角運動量は半奇数、右辺は整数となり、反応の前後で角運動量の保存が成り立たない。
　1931年パウリ（V. Pauli）は、β壊変の際に電子とともに電気的に中性なほとんど質量のない粒子が放出され、全体としてはエネルギーが保存されると仮定し、β壊変におけるエネルギーと角運動量の保存に関する問題に答えを与えた。この粒子をニュートリノといい、電子とともに放出される粒子を反ニュートリノ、陽電子とともに放出される粒子をニュートリノと名付けた。
　　　　中性子 → 陽子＋ｅ⁻ ＋ ν”（反ニュートリノ）
　　　　陽子　→ 中性子＋ｅ^＋＋＋ ν（ニュートリノ）
　1934年、フェルミ（E. Fermi）は量子力学的にこの問題を解釈し、ニュートリノはスピン1/2、ディラックの方程式を満足し、電気的に中性、フェルミ統計に従い、質量は0または電子に比べて極めて小さい粒子であるとした。ニュートリノという粒子は、他の粒子との相互作用が非常に弱いため、検出が困難であるが、現在ではその存在が実験で確認されている。

３．β壊変エネルギー
　β壊変エネルギーＱは、電子とニュートリノの運動エネルギーの和である。

　　　　Ｑ＝Ｅe ＋Ｅν　　　　　　　　　　　　　　　　　　　　　（1）

　ＥeとＥνは、それぞれ独立には定まらない。したがって放出される電子のエネルギーは、図１に示すようにある範囲にわたって連続的に分布し、その最大値ＥmaxはＥν＝０のときである。
　陽子Ｚ個、中性子Ｎ個の中性原子の質量をＭ_Z，Nとし、電子の質量をｍとすると、β⁻壊変の際のエネルギー保存の式は、

　　　　Ｍ_Z，N ｃ² ＝Ｍ_{Z＋1，N−1} ｃ² ＋Ｑ　　　　　　　　　　　（2）

したがって、β−壊変が起こるためのエネルギー条件は、

　　　　Ｑ＝（Ｍ_Z，N−Ｍ_{Z＋1，N−1}）ｃ² ＞０　　　　　　　　　　　　（3）

同様に、β＋壊変に対しては、

　　　　Ｑ＝（Ｍ_Z，N−Ｍ_{Z−1，N＋1} −２ｍ）ｃ² ＞０　　　　　　　　（4）

軌道電子捕獲に対しては、

　　　　Ｑ＝（Ｍ_Z，N−Ｍ_{Z−1，N＋1}）ｃ² −Ｉ＞０　　　　　　　　　（5）

となる。ここでＩは軌道電子の束縛エネルギーである。

４．β壊変とγ線
　β壊変においては、γ線の放出を伴う場合が非常に多い。β壊変後の娘核種、または核反応で生成された残留核は、しばしば励起状態にある。励起状態にある核は、より安定な低いエネルギー状態へγ線を放射して遷移する。なお、このγ線の放射はβ壊変そのものに直接関係はない。
　ある核が図２に示したような壊変型（壊変スキーム）で崩壊する場合、β線のエネルギー分布は複雑になる。ＡからＢ＊への遷移とＡからＢへの遷移は別のものであり、その各々にエネルギーβ1、β2のβ線が付随する。したがって全体のエネルギー分布は図３に示すようにその合成になる。ＢとＢ＊のエネルギーの差をεとし、ＭB、ＭB＊を核が基底状態Ｂにあるときと、励起状態Ｂ＊にあるときの質量とするとＭB＊ｃ² − ＭB ｃ² ＝ ε となり、β1のＥmaxと、β2のＥmaxは丁度εだけ異なる。β1とβ2の割合は、各壊変の起こる確率によって決まる。

５．崩壊定数
　β壊変における崩壊定数λまたは半減期Ｔは、次式で与えられる。

　　　　λ＝（ln2）／Ｔ＝（定数×マトリックス要素）・ｆ＝C・f　　　　　（6）

関数ｆは、多くの人により計算され、表あるいはグラフで与えられている。Cは遷移の確率をあらわすマトリックスを含む数である。
　（6）式を書きかえて、fＴ＝0.693/Cとするとわかるように、fＴが小さいほど、崩壊確率が大きいことを示している。

＜図／表＞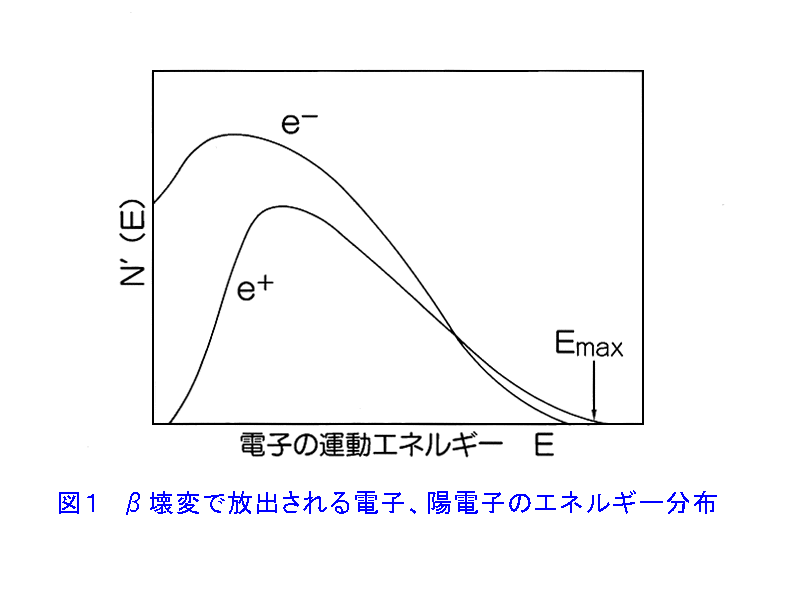

＜関連タイトル＞
半減期 (08-01-01-04)
α壊変 (08-01-01-05)

＜参考文献＞
（1）菊池正士他；原子核物理概論・中性子、共立出版、（1958）
（2）岩波　理化学事典（第４版）、岩波書店、（1987）
（3）山田勝美、森田正人、藤井昭彦　共著；ベータ崩壊と弱い相互作用、新物理学シリーズ15、培風館、（1974）
（4）石森富太郎編；原子炉工学講座Ｉ，原子核工学基礎、培風館、（1972）