|
＜大項目＞ 放射線利用 ＜中項目＞ 放射線利用の基礎 ＜小項目＞ 放射線の種類 ＜タイトル＞ α壊変 (08-01-01-05)
＜概要＞
原子核がα粒子を放射して、原子番号が2、質量数が4だけ小さい別の種類の原子核に変わる過程をα壊変という。α粒子はヘリウムの原子核である。α壊変をする性質を持った原子核をα放射性核またはα放射体という。α放射体にはラジウム、ウラン、トリウム等、天然に存在するものの他に、カリホルニウムのように人工的に作りだされるものもある。 ＜更新年月＞ 2002年03月 （本データは原則として更新対象外とします。） ＜本文＞ １．α壊変 α壊変は原子番号Ｚ、質量数Ａの原子核がα粒子を放出して原子番号Ｚ-2、質量数Ａ-4の原子核に変わる過程をいう。言いかえれば、陽子2個、中性子2個からできているα粒子が飛び出していったあとには、陽子が2個減って、原子番号が2だけ小さい原子核が残る。また、中性子も2個減るので質量数は合計で4だけ減少する。1909年ラザフォード（Ernest Rutherford）とロイズ（Thomas Royds）は、α粒子がヘリウム（4He）原子核であることを証明した。半減期はそれぞれの核種に特有で、短いものは214Po → 210Pbの1.64×10−4秒、長いものは238Ｕ → 234Thの4.47×10＋9年など様々である。 ２．α壊変のエネルギー α壊変が起こるために必要なエネルギーの条件は、 Ｑ＝［ＭZ，N−（ＭZ-2，N-2＋Ｍ2，2）］ｃ2＞0 （1） である。ここで、ＭZ，N、ＭZ-2，N-2、Ｍ2，2は、親核、娘核、α粒子のそれぞれの質量数で、ｃは光の速度である。Ｑはこの壊変によって解放されるエネルギーで、壊変エネルギーといい、α粒子及び反跳された娘核の運動エネルギーの和、 Ｑ＝（1/2）・Ｍ2，2 ｖ2＋（1/2）・ＭZ-2，N-2 Ｖ2 （2） に等しい。ここで、ｖはα粒子の速度、Ｖは娘核種の速度である。下式の運動量保存則 Ｍ2，2 v＝ＭZ-2，N-2 Ｖ （3） を用いて、（2）式を解けば、α粒子の運動エネルギーＥαは、 Ｅα＝（1/2）・Ｍ2，2 ｖ2＝Ｑ/［1＋Ｍ2，2／ＭZ-2，N-2］ （4） で与えられる。 α壊変をする核種の質量数ＭZ，Nは、一般にα粒子の質量数Ｍ2，2＝4に比べて極めて大きいので、（4）式のＭ2，2/ＭZ-2，N-2＜＜1となり、Ｑは殆どα粒子の運動エネルギーに等しくなる。すなわち、α壊変の場合、α粒子のエネルギーは一定である（β壊変の場合には、電子とニュートリノが放射されるため、両粒子とも放出エネルギーは均一ではない）。 図１ は210Poから放射されるα粒子の飛跡をウイルソン（C.T.R，Wilson）の霧箱で撮影したものである。気体中の飛跡の長さがだいたい同じであるのはエネルギーが均一であることを示している。この距離のことを飛程という。α粒子の空気中の飛程（Ｒ cm）とエネルギー（Ｅα MeV）との間には、 Ｒ＝ａＥα3/2 （5） の関係がある。したがって、空気中の飛程がわかれば、α粒子のエネルギーを推定できる。また逆に、α粒子のエネルギーが測定できれば、その空気中での飛程がわかる。 ある場合には、1種類のエネルギーのα粒子だけでなく、2種またはそれ以上の種類のエネルギーを持ったα粒子を放出する核種がある。 表１は228Thの娘核212Biが208Tlにα壊変するときに放出されるα粒子のエネルギースペクトルを示したものである。これは娘核（212Bi）が直ちに基底状態（208Tl）に移らず、種々の励起状態に遷移し、そのエネルギー準位に対応したエネルギーを放出するためである。この場合Ｑがそれだけ小さくなり、α粒子のエネルギーも小さくなる。この時α壊変に続いてγ線の放射が起こる。放出されるγ線のエネルギーはＱの小さくなった分に等しい。 ３．飛程と壊変定数（ガイガー・ヌッタルの法則） 212Poから放出されるα粒子の飛程は約8.6cm、232Thのそれは約2.8cmである。α壊変の半減期は、前者が3.04×10−7秒、後者が1.41×10＋10年である。ガイガーとヌッタルは、α粒子の飛程が長いほどα壊変の半減期は短いという実験的事実に着目し、1911年に飛程（Ｒ）とと壊変定数（λ）に関する多くの測定値を整理し、次式の関係式を導いた。 logλ＝ａ・logＲ＋ｂ （6） ここでａおよびｂはと壊変系列によってきまる定数である。λはλ＝（ln2）/Tなる式で半減期（Ｔ）と関係している。（6）式をガイガー・ヌッタル（Geiger-Nuttall）の法則という。 飛程はα粒子のエネルギーが高いほど長い。したがって、α粒子のエネルギーが高いほど壊変定数が大きいといえる。これは大きいエネルギーを持ったα粒子は原子核から飛び出す力が大きいし、また核内での振動回数も多いので、核外に飛び出す機会が大きくなると解釈できる。 α粒子が核の中から外へ出るには、Ｚ＞82の核については20MeV以上の高さのクーロン障壁を通らなければならない。このことはエネルギーが数MeVのα粒子にとっては、古典力学的には不可能であると考えられた。1928年、ガモフ（George Gamow）等は、障壁の中をα粒子がしみ出すいわゆるトンネル効果という概念を導入し、量子力学的取扱いによってこれを解釈した。 ＜図／表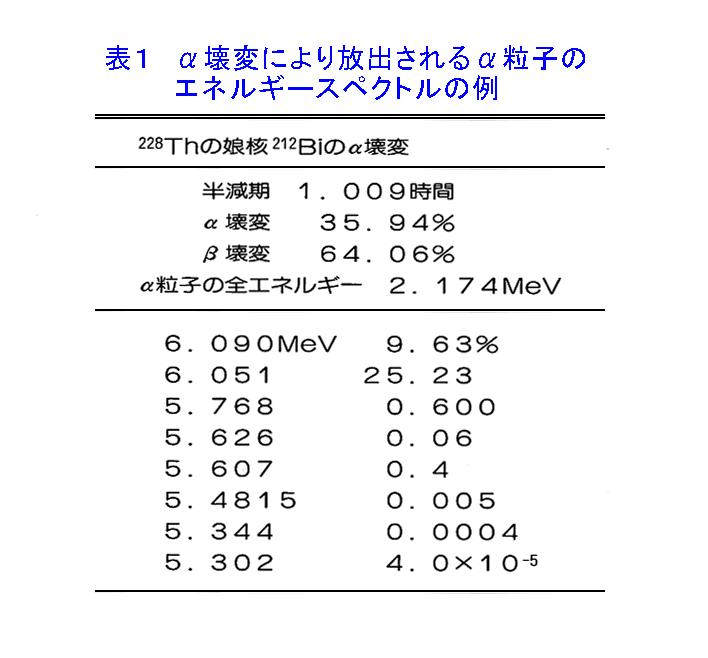＞ 表１ α壊変により放出されるα粒子のエネルギースペクトルの例 図１ 210Poより放出されるα粒子の飛跡のWilson霧箱による写真 ・図表を一括してダウンロードする場合は ここをクリックして下さい。
＜関連タイトル＞ 半減期 (08-01-01-04) β壊変 (08-01-01-06) ＜参考文献＞ （1） フェルミ著、小林稔等訳；原子核物理、物理学叢書、吉岡書店、（1966） （2） 岩波 理化学事典（第４版）、岩波書店、（1987） （3） 石森富太郎編；原子炉工学講座Ｉ，原子核工学基礎、培風館、（1972） （4） 菊池正士他；原子核物理概論・中性子、共立出版、（1958）
|
