|
<解説記事ダウンロード>
<概要>
物体は、どんな形ででも、エネルギーを吸収したり放出したりすると、E=MC2の式に基づいて、その質量も増加したり減少したりする。1905年アインシュタインは特殊相対性理論を発表し、このことが基本原理から導出されることを示した。この導出過程を思考実験の形で述べる。 <更新年月> 1998年05月 (本データは原則として更新対象外とします。)
<本文>
1.はじめに 1905年、アインシュタイン(Albert Einstein、独、1879〜1955)は、特殊相対性理論を発表した。この理論から導かれる重要な結論として、「物体は外からエネルギーEを吸収すると、質量はE/C2(Cは光速である)だけ増加する。」という法則がある。この法則をわかりやすく説明するために、以下に示す思考実験が考案された。 2.エネルギー吸収の思考実験 1) 図1 (a)に示すように、座標系K0 において静止物体Bに左右から光S、S’が入射する。光は両者共、エネルギーE/2を持つ。運動量ベクトルは両者反対向きで絶対値は共にE/(2C)である。 物体が光を吸収した後を考えると、両方から入射してくる光の運動量ベクトルの和はゼロであり、光を吸収した後も物体は静止している。 2)座標系K0 に対して下向きに速度V(簡単のためにVがCより十分小さいとして、以後、高次の無限小を無視する)で動いている座標系Kに移り、上記の光の吸収を考察する。物体Bは、吸収の前後共にK0 座標系で静止していたわけだから、K座標系で観ると吸収の前も後も共に速度Vで上向きに動く。入射する光は、図1(b)に示すように水平方向に対して角度アルファをもって入射する。ここにsinアルファ=V/Cである(このことは、地球に恒星から光が到達する際の光行差として実験的にも確かめられている)。 3)両側から入射する光は、それぞれ上向きの運動量成分として(E/2C)sinアルファを持つ。これは(E/2C)・(V/C)に等しいから、両側からの入射分を加えて、上向きの運動量成分の合計は(E/C2)・Vとなる。 光を両側から吸収すると、物体は吸収前のMVに光の吸収によって得た(E/C2)・Vを加えた上向き運動量成分を持つことになる。これは、(M+(E/C2))Vに等しい。 光を吸収した物体の質量をM’とすると、これは上向きに速度Vで動き、上向き運動量成分M’Vを持つ。運動量保存則によって、これは先程求めた(M+(E/C2))Vに等しくなければならない。このことから、M’=M+(E/C2)が導かれる。すなわち、光の吸収の形でエネルギーEを得た物体は、質量が(E/C2)だけ増加している。 3.質量とエネルギーの関係 以上の思考実験からわかることは、どんな形にせよ物体がエネルギーEを外から取り込んだ場合には質量がE/C2だけ増加し、エネルギーEを外へ放出した場合には質量がE/C2だけ減少することである。 このことを、例えば炭素と酸素が化合して炭酸ガスになる化学反応の場合に当てはめてみると、化合した炭素と酸素が炭酸ガスになった際に燃焼熱が放出されたことによって失われる質量は、元の質量の(化合した炭素と酸素の質量の和)の10のマイナス10乗程度にしかならない。 一方、原子炉内で起こるウラン235の核分裂反応では、ウラン235の原子核は2つの核分裂生成物の原子核と2個程度の中性子に分裂するが、反応後の質量は元のウラン235の質量の1000分の1程度小さくなっており、この減少した質量から核分裂の際に解放されたエネルギーが計算される。一般に、核反応では質量の増減は測定が可能で、この質量の変化分から核反応の際に放出されたり吸収されたりするエネルギーを求めることができる。 <図/表> 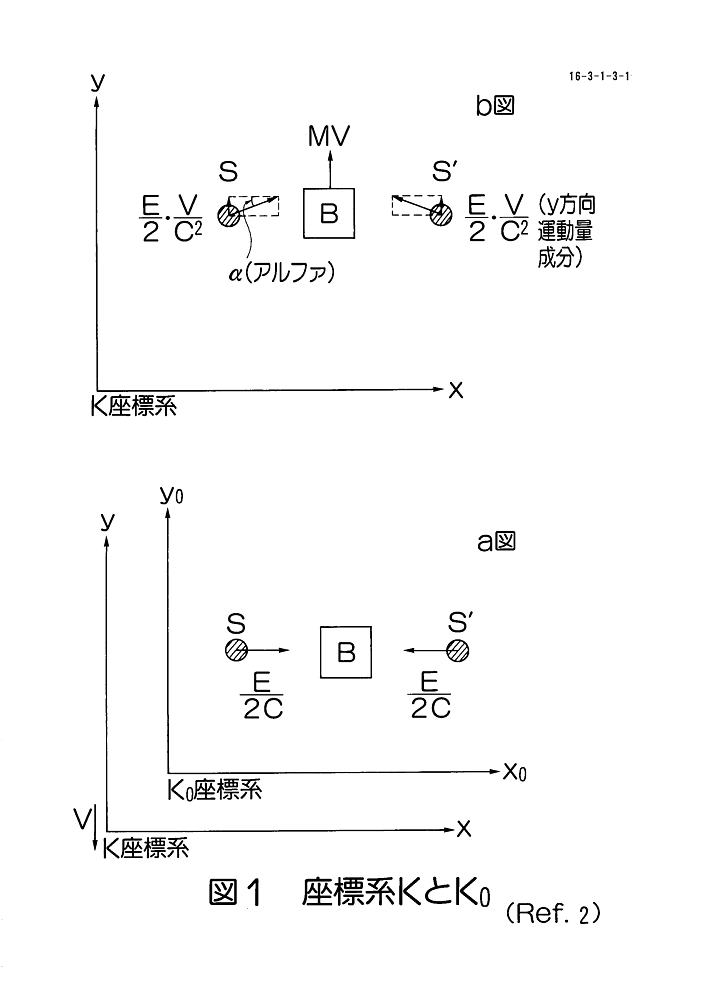
<関連タイトル> 運動エネルギーによる質量増加の検証となったカウフマンのベータ線屈曲の実験 (16-03-03-02) トムソンとアストンによるネオン同位体の発見と質量分析器の開発 (16-03-03-04) 原子力・放射線にかかわるノーベル賞受賞者 (16-03-03-13) <参考文献> 1.物理学古典論文叢書4、 相対論、 東海大学出版会、 1969年、 35?37頁 2.H.A. Boorse and L. Motz, The World of the Atom, Basic Books, Inc.(1966)581-584
|

