Ｘ線反射率法と”埋もれた”界面の科学 (08-04-01-33)

＜本文＞
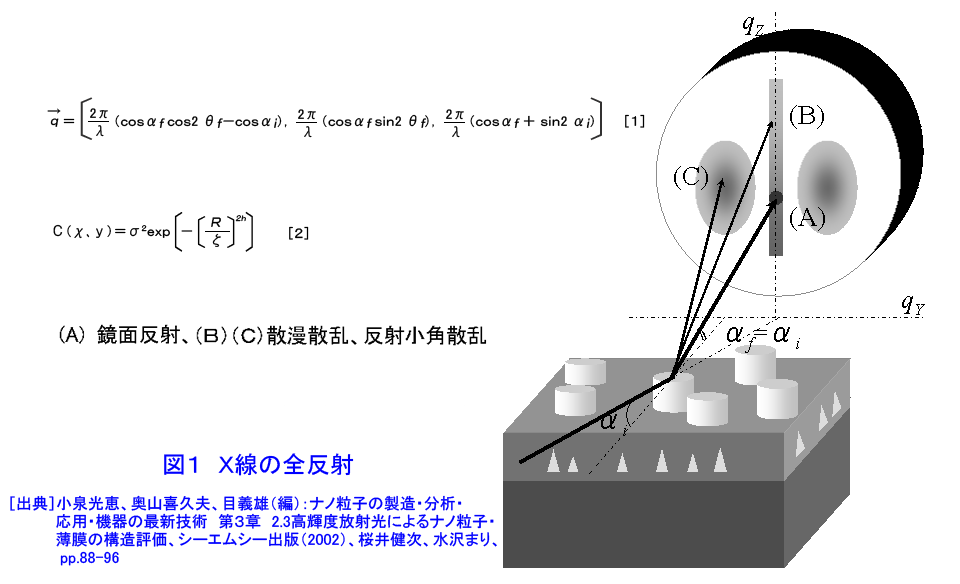
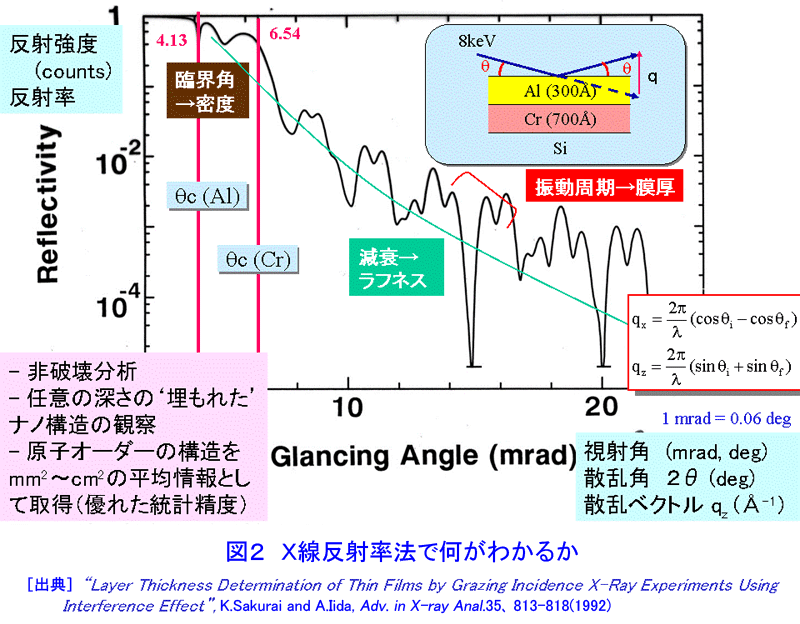
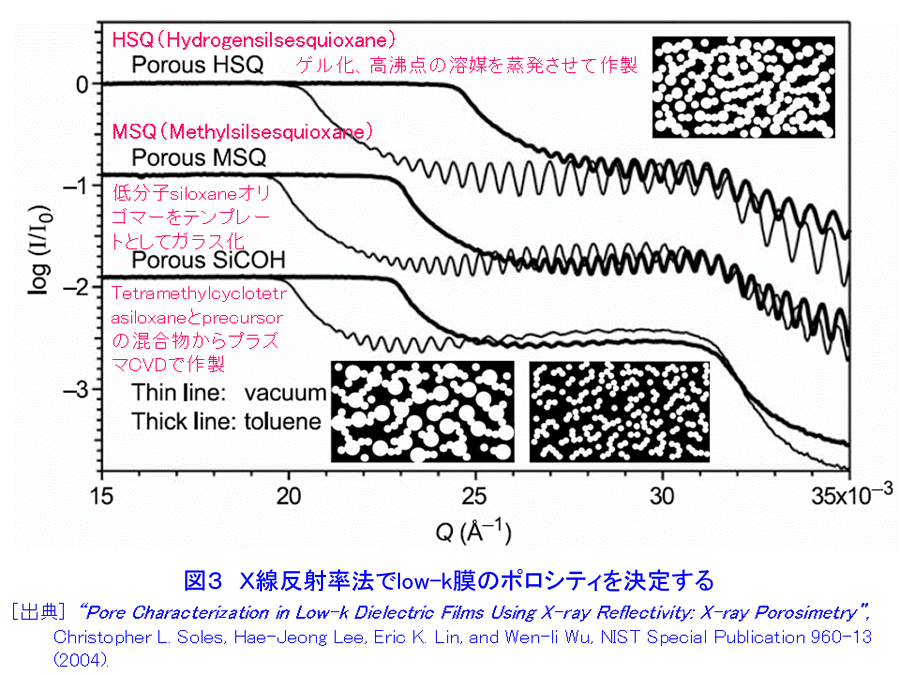
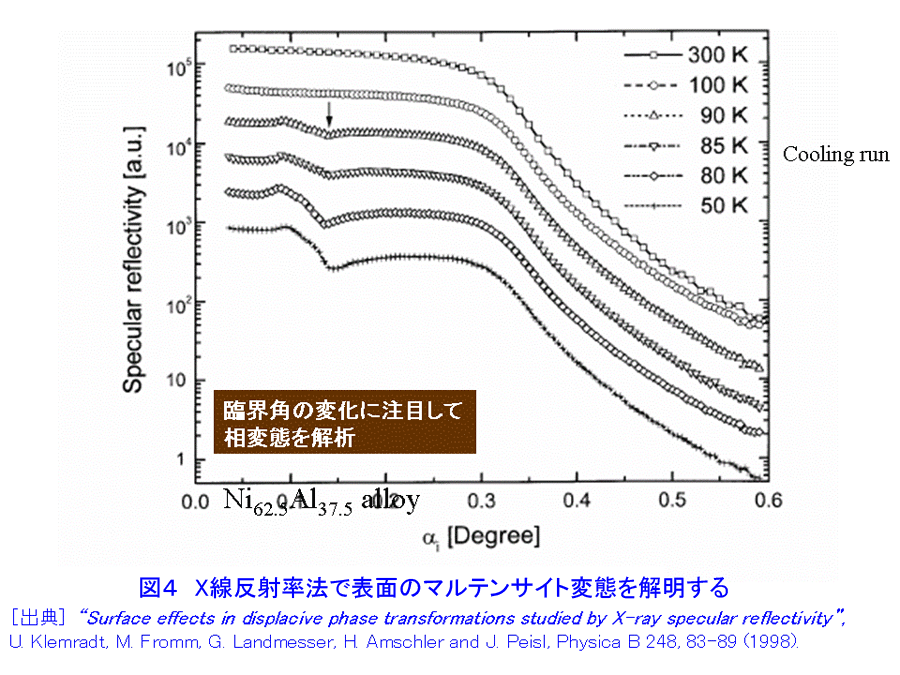
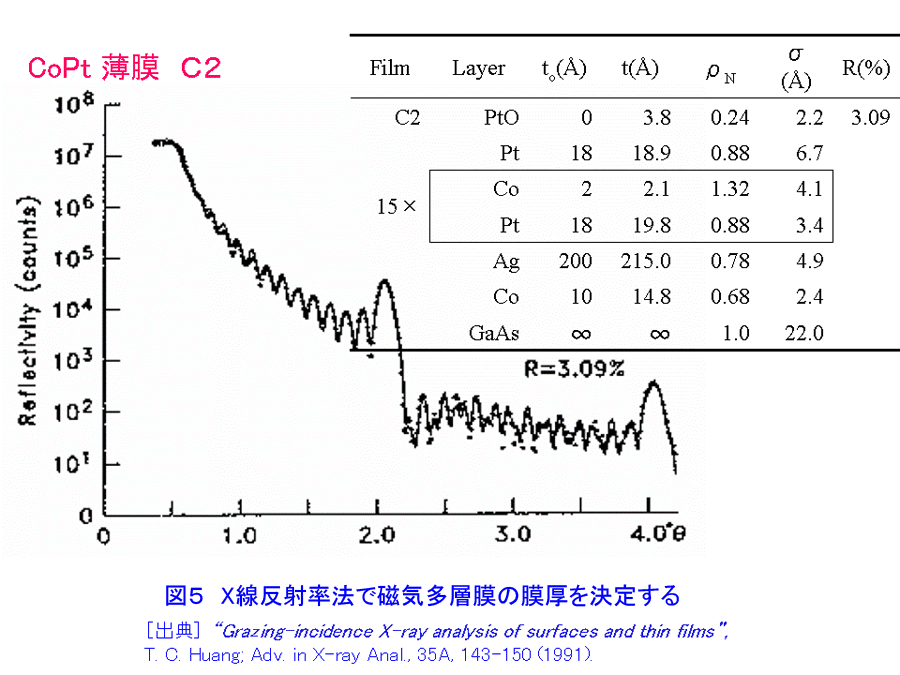
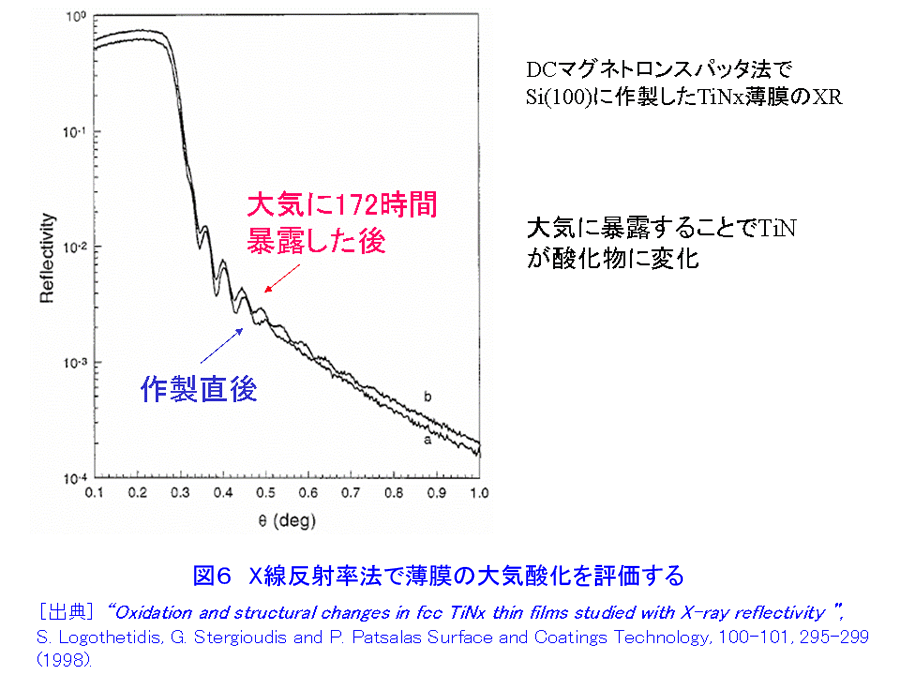
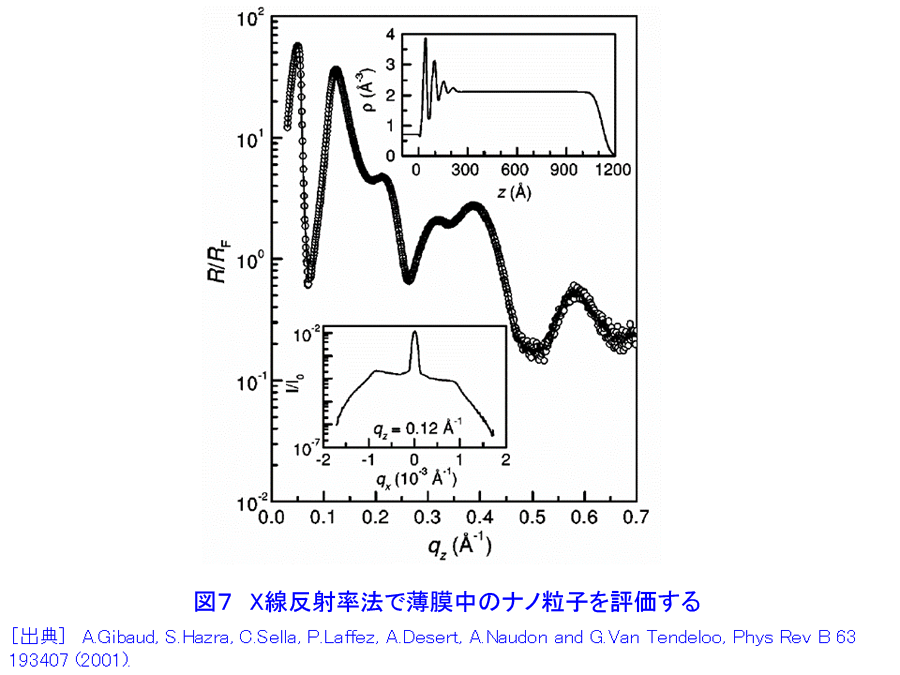
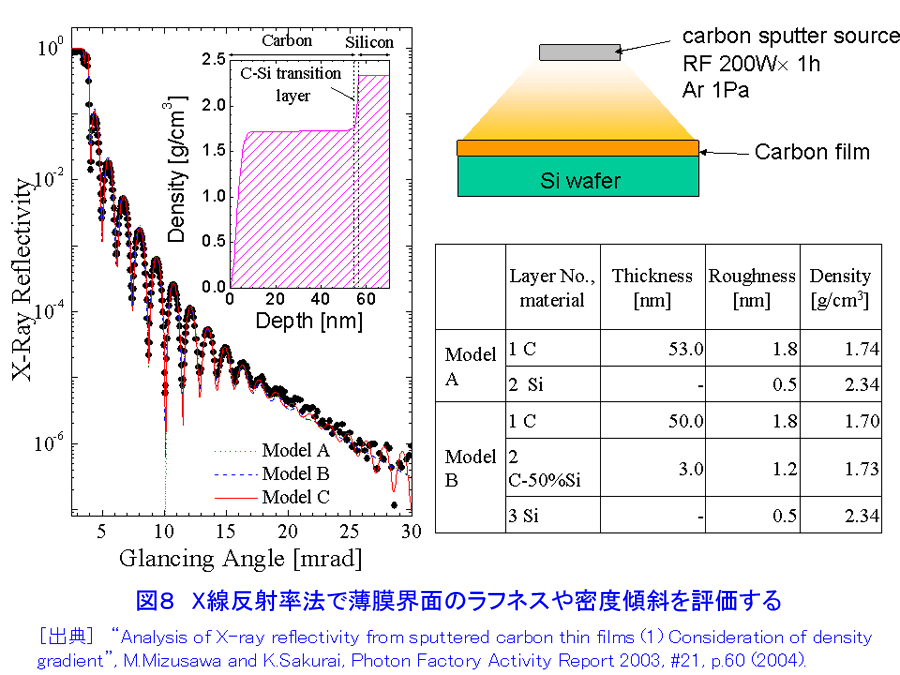
１．”埋もれた”界面の科学へのアプローチ
　これまでの表面科学の研究は、物質の最表面構造と物性に関するものが多い。金属・半導体・磁性体等の多層膜界面、保護層のついた量子ドット、接着界面等、表面に露出していない”埋もれた”構造は、諸現象の基礎科学的な理解の面でも、産業応用の観点でも、最表面構造に勝るとも劣らず重要であるが、研究の数が必ずしもあまり多くないのは、手段が限られていることによると考えられる。まさに”埋もれている”がゆえに、表面に敏感なほとんどの研究手法を使うことができないのである。他方、ナノサイエンス・テクノロジーの進展に伴い、ナノドット等、さまざまな”埋もれた”ナノ構造が広汎に作製されるようになってきた。その評価には、次のような要素が重要と考えられている。（i）　非破壊性、（ii）「部分」と「全体」の連関の考察（「木」も「森」も見る」）、（iii）「ものつくり」「機能発現」とのリンケージ（「生きた」測定・解析）
　Ｘ線・放射光および中性子は、最表面にも表面より深い領域にも応用可能な優れたプローブであり、原子レベルの構造情報であってもmm〜cmの広い試料面積を照射して得ていることや、試料環境や雰囲気を制御する技術と組み合わせることが比較的容易であること等の利点があり、”埋もれた”構造の研究に本格的に活用されることが望まれる。
２．Ｘ線反射率法について［文献1-5］
　物質のＸ線に対する屈折率は1よりわずかに小さい値を持ち、平坦かつ平滑な物質表面に全反射臨界角θcよりも浅い角度で入射したＸ線は物質の外部で光学的な全反射を生じる。全反射条件の近傍では、Ｘ線の侵入深さは数ナノメートルから数100ナノメートル程度であり、またその程度は角度によって調整することができる。多くのナノ構造は、何らかの基板の上に作製される場合が多いが、こうした全反射の条件の近傍では、侵入深さが浅いため基板の影響を抑えた測定が可能である。
　物質表面でＸ線が全反射を起こすとき、図１に示すように、試料表面と入射Ｘ線のなす角と等しい角度で生じる強い反射スポット（鏡面反射（specular reflection）と呼ばれる。図中の（A））の他にも、弱い散乱Ｘ線（図中の（B）や（C））が観測されることが知られている。これらは、散漫散乱（diffuse scattering）または反射小角散乱（GISAXS（grazing-incidence small angle scattering））と呼ばれ、本来は統一的に扱われるべきものでありながら、実験方法・装置の違いや研究の歴史的な背景を反映して、現状では、両者の名称はしばしば区別して使用されている。
　入射Ｘ線の進行方向をX軸、これに直行するようにY，Z軸をとり、Ｘ線と試料の幾何学的な関係を考慮すると、散乱ベクトルqは
q＝（2π/λ(cosαfcos2θf−cosαi), 2π/λ(cosαsin2θf), 2π/λ(sinαf＋sinαi))　　　　（1）　（図１参照）
のように書ける。ここで、αi，αfは、試料表面と入射Ｘ線、散乱Ｘ線のなす角で、2θfは、散乱Ｘ線の試料表面への投影が入射Ｘ線進行方向（X軸）となす角である。鏡面反射では、αf＝αi、2θf＝0なので、常にqx＝qy＝0 で qz＝4πsinαi/λになる。通常は、αiを変化させ、それにあわせて検出器の位置も動かして、ちょうどＸ線回折のθ/2θ走査による測定のようにして鏡面反射率の角度依存性を求めることが多い。鏡面反射が急速に落ちる角度（臨界角）の位置から表面近傍の密度、臨界角よりも高角域に現れる干渉縞の周期から薄膜の各層の平均厚さ［文献6］、鏡面反射の減衰の度合いや干渉縞の振幅等、プロファイルの形状からラフネスや界面の急峻さ［文献7］を評価することができる（図２）。
　鏡面反射率の測定方法・装置を拡張して、反射スポットの周囲の微弱な散乱を測定する実験は、（1）式において、αf≠αi、2θf＝0の条件で、非常に多く行われていて、広く散漫散乱の名称で知られている。この場合で、特に、αiを固定し、検出器だけを鏡面反射の周囲を動かしてプロファイルを測定すると、図１の（B）にあたる散乱Ｘ線を測定することになる。通常、検出器スキャン（detector scanまたはradial scan）と呼ばれる測定法である。この他、逆に検出器を固定して、試料のみを回転させるロッキングスキャン（rocking scan またはtransverse scan）や、鏡面反射位置から検出器を常に決まった角度だけずらして測定するオフセットスキャン（offset scan またはlongitudinal scan）も行われる。鏡面反射がqzの走査により得られ、従って深さ方向の変化に敏感であるのに対し、これら散漫散乱は水平な成分を含んでおり、面内方向の情報を反映する。特に、表面や薄膜界面のラフネスになんらかの相関があることにより生じると考えられる。自己相似モデルが多くの実例であてはまることが知られており、任意の座標（x， y）におけるz方向の位置（表面からの高さ）についての相関関数は、rms表面粗さσを用いて、
C(x, y)＝σ2 exp(−(R/ξ)2h)　　（2）　（図１参照）
のように記述され、他方、散漫散乱の理論的な強度式はDWBA（Distorted Wave Born Approximation）を考慮して与えることができるので［文献8］、実測データとのフィッティングにより、構造パラメータを決定することができる。Ｘ線小角散乱は、数度の回折角範囲内に観測される散乱であり、物質内の数原子あるいはそれ以上の距離の長範囲にわたる電子密度の空間的変化に起因して生じる。粒子のサイズや粒子間の距離等を直接反映することから不均一系の構造解析に長い研究の歴史があり、測定には透過法の配置をとるのが一般的である。反射小角散乱［文献9，10］は、透過型小角散乱の解析技術・装置［文献11，12］を図１のように修正し、（C）のような散乱Ｘ線を1次元または2次元の検出器やカメラシステムで測定する手法を出発点として研究が始まった。従って、αf≠αi、2θf≠0であり、αiは固定され、通常走査されない。
　Ｘ線反射率法は、実験室系のＸ線管等を用いて行うことができるが、放射光を利用すると（i）強度が桁違いに強い、（ii）任意のＸ線波長を選べる、（iii）平行性が高く発散が小さいため、光学系によるロスが少ない、（iv）偏光・パルス性を利用する計測が可能等、多くの魅力的な利点があり、ナノサイエンス・テクノロジーにおける構造解析に大いに効用がある。
３．Ｘ線反射率法の応用
　Ｘ線反射率の応用範囲はきわめて広く、ほとんどどんな薄膜でも、あるいは基板でも測定対象になりうる。臨界角は表面近傍の密度に敏感であることから、low-k 材料のポロシティの決定に有効である。図３に3種類の low-k 膜のＸ線反射率データを示した。それぞれについて、そのままの状態とトルエンを吸着させた後の結果を表示している。横軸の低Q側ではいずれもフラットな全反射領域であるが、反射率が急激に落ちるQの位置（臨界角）は密度によって違っている。トルエンを吸着すると、密度が増加して高Q側に大きくシフトする。臨界角よりも高Q側では、層の厚さに対応した干渉パターンが現れる。トルエンの吸着により膨潤し、密度だけでなく層の厚さも変化していることがわかる。表１はこのようなデータからポロシティを決定した結果を示している。もう1例、興味深い密度決定の例を示す。ドイツ、ミュンヘンのPeisl教授のグループは、表面のマルテンサイト変態をＸ線反射率法により解明した［文献13］。図４は、電解研磨で得られたNi62.5Al37.5(001)表面のＸ線反射率を、試料を冷却しながら測定した結果である。同一試料のバルクの変態温度である85Kより高い90Kで、0.14°近傍に変曲点が認められた。加熱過程ではヒステリシスがあり、同じ温度であっても図４とは異なる結果が得られる。Ｘ線回折法による検討から判定できるバルクのマルテンサイト変態温度は85Kであり、またヒステリシスは認められない。すなわち、バルクのマルテンサイト変態は二次相転移だが、表面のマルテンサイト変態は一次相転移のような挙動を示し、かつ変態温度も高いことが明らかにされた。
　冒頭で述べたとおり、Ｘ線反射率法では表面の下にある「埋もれた」界面の情報を非破壊的に得られる点が他の方法よりも優れている。図５はCo/Pt 磁性多層膜の層構造を決定した例である。界面における屈折率の違いから、多重反射が生じ、それらの干渉により、Ｘ線反射率のデータには複雑な干渉縞が現れる。周期多層膜の場合には、その周期に対応したブラッグピークが得られる。モデル計算と実験値とのフィッティングにより、各層の膜厚や界面のラフネスを決定することができる。図６は、DCマグネトロンスパッタ法でSi(100) に作製したTiNx薄膜を大気中に放置したときの経時変化をＸ線反射率法により調べた結果である。大気酸化により、窒化物薄膜の一部が酸化物に変わり、また膜厚自体も変化している。このようなきわめてわずかな変化を敏感に検出できること、出来上がった後の薄膜について、破壊することなく、このような変化をモニターし続けられること等は、まさにＸ線反射率法の強力な点である。薄膜中のナノ粒子の解析に用いた例を次に示す。太陽光の可視・赤外の波長成分を効率よく吸収させる目的でセラミック・メタル薄膜の研究が行われている。Al2O3やSiO2の絶縁体マトリックス中にPt等の貴金属ナノ粒子を不均一に分散させて作製され、良い特性を得るためにさまざまな試みがなされているが、詳細な構造はほとんど知られていなかった［文献14，15］。図７は、フランスのGibaud らによる鏡面反射率の測定結果とそこから得られた電子密度分布（挿入図〔上〕）、ロッキングスキャン散漫散乱プロファイル（挿入図〔下〕）を示している。解析の結果、直径3.1nm の球形粒子が平均距離5.8±0.8nmで全膜厚120nm のなかで分散しており、他方、表面近傍はラフネスが3.4nm と大きく、更に基板のごく近くでは粒子が層状構造を取っていることが明らかになった。こうした検討は、半導体量子ドット等にも同様に適用することができる。ほぼ同じ条件で作製された複数の試料について、キャップ層をつけた後に、Ｘ線反射率法のような非破壊的な方法で構造を調べ、相互に比較検討することは作製技術に関わる研究の観点で意義が大きい［文献16］。最後に、”埋もれた”薄膜界面のラフネスや密度傾斜をＸ線反射率で検討した例を示す。図８は、スパッタ法で作製されたカーボン薄膜のデータである。スパッタ法ではきわめて低密度の薄膜が得られるが、モデル計算の結果と最もよく適合するのは、図中に示したAやBのような単純なモデルではなく、CのようにSi基板との間に密度が傾斜したなだらかな界面を考慮した場合であった。これまで、単純な層構造だけをまず考慮し、そこで説明がつかない部分をガウス型の界面ラフネスで解釈しようというのが通例であったが、最近は、このように密度傾斜を検討した例を含め、積極的に界面の詳細な形状を議論しようとする機運が理論、実験両面で高まっている。

＜図／表＞

＜参考文献＞
（1）株式会社アグネ技術センター：金属、Vol.74、No.3、p.305 （2004）.
（2） Als-Nielsen and D. McMorrow， ”Elements of Modern X-Ray Physics”， John Wiley ＆ Sons， London （2001）.
（3） K.Stoev and K.Sakurai， Spectrochim. Acta B54， 41 （1999）.
（4） M.Tolan，”X-ray Scattering from Soft-Matter Thin Films”， Springer， Berlin （1999）.
（5） J.Daillant and A.Gib aud Eds.:”X-ray and Neutron Reflectivity: Principles and Applications”， Springer （1999）．
（6） L.G.Parratt， Phys. Rev.， 95， 359 （1954）.
（7） L.Nevot and P.Croce， Rev. Phys. Appl.， 15， 761 （1980）.
（8） S.K.Sinha， E.B.Sirota， S.Garof， and H.B.Stanley， Phys. Rev.， B38， 2297 （1988）.
（9） J.R.Levine， J.B.Cohen， Y.W.Chung and P.Georgopoulos， J. Appl. Cryst.， 22， 528 （1989）.
（10） A.Naudon， T.Slimani and P.Goudeau， J. Appl. Cryst.， 24， 501 （1991）.
（11） A.Gunier and G.Fournet， ”Small Angle Scattering of X-ray”， John Wiley ＆ Sons，London （1955）.
（12） O.Glatter and C.Kratky， ”Small Angle X-ray Scattering”， Academic Press，（1982）.
（13） U.Klemradt， M.Fromm， G.Landmesser， H.Amschler and J.Peisl， Physica B 248， 83 （1998）.
（14） S. Hazra， A. Gibaud， A. Desert， C. Sella， and A. Naudon， Physica B 283， 97 （2000）.
（15） A.Gibaud， S.Hazra， C.Sella， P.Laffez， A.Desert， A.Naudon and G.Van Tendeloo， Phys Rev B 63 193407 （2001）.
（16） M.Mizusawa and K.Sakurai， Trans. Mater. Res. Soc. Jpn. 28， Special Issue （Nov. 2003）， 51-54 （2003）.